This article is in continuation of my earlier articles published on Virahanka numbers: Part 1 , Part 2 , Part 3
How many metrical forms with r Gurus are there in a n matra prastaar?
We know that a Guru has 2 matras, hence the number of Laghus in the metrical forms having r Gurus in a n matra prastaar will be = n – 2r.
Therefore, the number of syllables will be = r + n – 2r = n – r.
Hence, the number of metrical forms with r Gurus in a n matra prastaar is
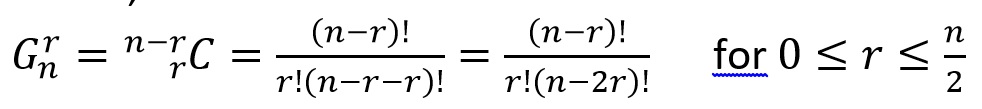In a n matra prastaar the metrical forms cannot have more than n/2 Gurus.
Now, let us find the number of metrical forms with 2 Gurus in a 6 matra prastaar:
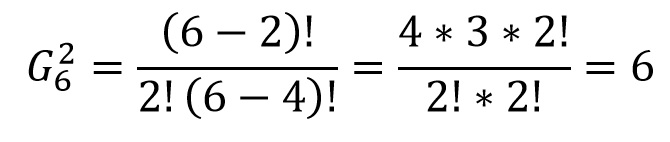
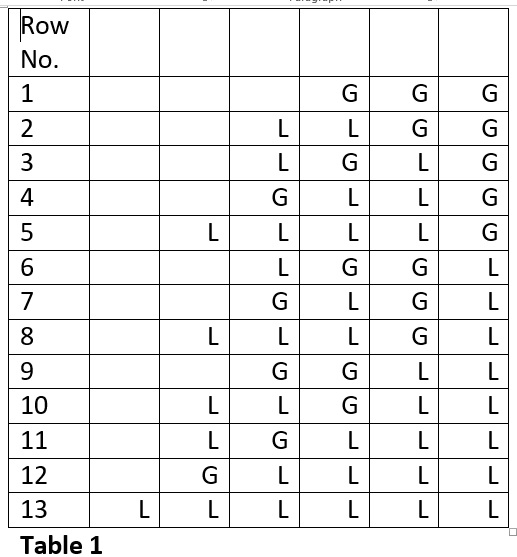
You can verify this answer in a 6 matra prastaar given in Table 1.
In my earlier article, I had discussed Pingala’s Meru prastaar.
Meru prastaar is a table which lists the number of meters with different number of Laghus (or Gurus) in a quarter with n syllables (varna vrutta).
Damodara has given a method to construct such a table called Matra Meru for matra vrutta in his book Vanibhusana. Before presenting Matra Meru I will discuss some basics.
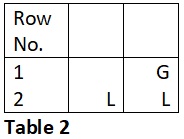
Let us consider a 2 matra prastaar. It cannot have a metrical form with 1 Laghu. It will have metrical forms with either no Laghu or with 2 Laghus. Refer Table 2.
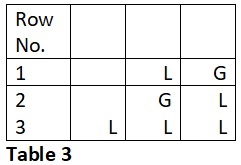
Now let us consider a 3 matra prastaar. There will be no metrical forms in a 3 matra prastaar that doesn’t have a Laghu. It will have metrical forms which have either 1 or 3 Laghus. It cannot have metrical forms with 2 Laghus. Refer Table 3.
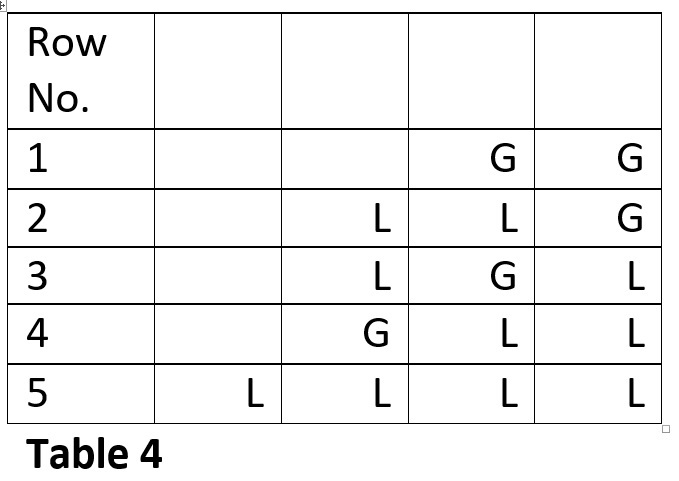
Now let us consider a 4 matra prastaar. It will have metrical forms with 0, 2 and 4 Laghus. It cannot have metrical forms with 1 or 3 Laghus. Refer Table 4.
In general in a n matra vrutta prastaar, if n is even the metrical forms will have only even number of Laghus. And if n is odd the metrical forms will have only odd number of Laghus.
Damodara’s sutra to construct the matra meru is:
द्वयं द्वयं समं कोष्ठं कृत्वान्त्येष्वेकमर्पयेत्।
एकद्विकत्रिकचतुःक्रमेण प्रथमेष्वपि॥
शीर्षाङ्काप्तपराङ्काभ्यां शेषकोष्ठान् प्रपूरयेत्।
मात्रामेरुरयं दुर्गः सर्वेषामतिदुर्गमः॥ (वाणीभूषणम् १.३७-३८)
- The successive rows of the matra meru have 1, 2, 2, 3, 3, 4, 4, … cells.
- Place a 1 in the top row and at the end of each row.
- Place a 1 at the beginning of all even rows and 2, 3, 4, 5, … at the beginning of odd rows.
- The other cells are filled by the sum of number in the cell immediately above and the number in the cell which is in the row further above and to the right.
Refer Table 5.
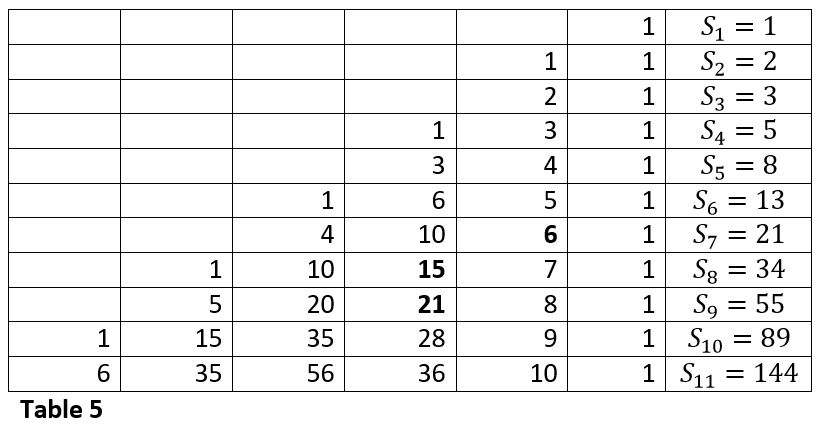From table 5, we can see that the 6 matra prastaar has 1 metrical form with 0 L, 6 with 2 L, 5 with 4 L and 1 with all 6 L. From the same prastaar we can see that there is 1 metrical form with all 3 G, 6 with 2 G, 5 with 1 G and 1 with 0 G.
We can see that the 7 matra prastaar has 4 metrical forms with 1 L, 10 with 3 L, 6 with 5 L and 1 with all 7 L. From the same prastaar we can see that there are 4 metrical forms with 3 G, 10 with 2 G, 6 with 1 G and 1 with 0 G.
Let us find the number of metrical forms that have 2 Gs in a 9 matra prastaar from the matra meru. We see that it is 21 = 15 + 6. This is shown in bold in Table 5. What is the logic behind this?
We have the combinatorial relation:
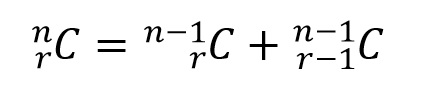
This was established by Halayudha Bhatt in his commentaries on Chandahshastra in his work Mritasanjeevani (composed in 10th century CE). Refer my earlier article: pingalas algorithm prastaar
We have
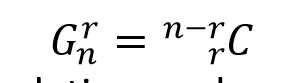
Using the above combinatorial relation we have
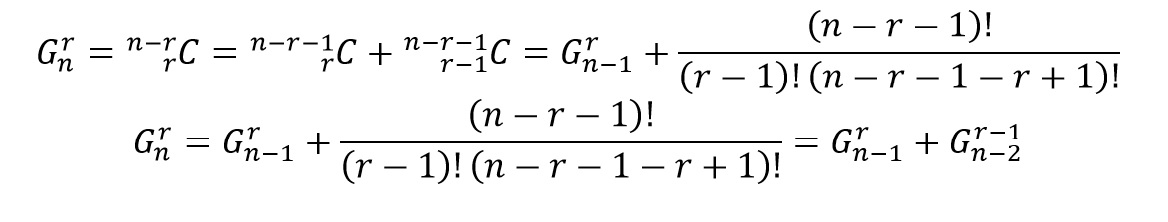
This relation is rule behind the construction of the Matra Meru.
This concludes my article series on Virahanka’s Numbers.
Disclaimer: The opinions expressed in this article belong to the author. Indic Today is neither responsible nor liable for the accuracy, completeness, suitability, or validity of any information in the article.
