This is in continuation of my earlier article:
https://www.indica.today/quick-reads/virahanka-numbers-i/
In my earlier article I had discussed Virahanka’s pratyay for Matra Prastaar. Now you must be wondering what is the logic behind Virahanka’s pratyay for Matra prastaar? To explain this I will use a tree graph to generate the combinatorial sequence for a quarter having n matras. To understand more about tree graphs kindly watch my video at:
https://www.youtube.com/watch?v=XmuJcGYmPHg&t=12s
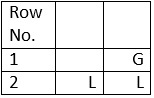
Table 1
To generate the matra prastaar for a quarter having 2 matras (refer Table 1) I will draw the Tree graph given in Figure 1.
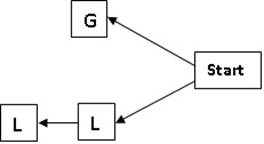
Figure 1
For the first position from the right (or last position from the left) there are two options – a G and an L. Here the branch that begins with a G ends there itself since the total value of matras is 2. For the second position from the right for the branch that begins with an L, there will be only one option that is an L. This branch of the tree will end here since its total matra value now is 2. If you now read and list all the branches from the left you get the matra prastaar for n = 2.
For the tree graphs used to generate the matra prastaar for quarter having n matras every node will have two branches – first one for G and second one for L. The branches end when their total matra values become equal to n. when we read and enlist every branch from the left we get the matra prastaar for a quarter having n matras.
To generate the matra prastaar for a quarter having 3 matras (refer Table 2) I will draw the Tree graph given in Figure 2.
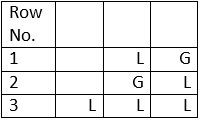
Table 2
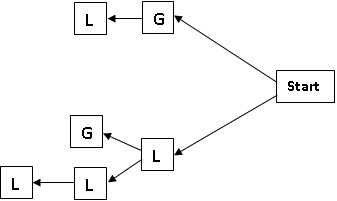
Figure 2
To generate the matra prastaar for a quarter having 4 matras (refer Table 3) I will draw the Tree graph given in Figure 3.
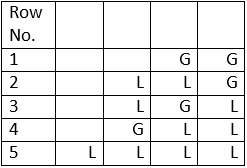
Table 3
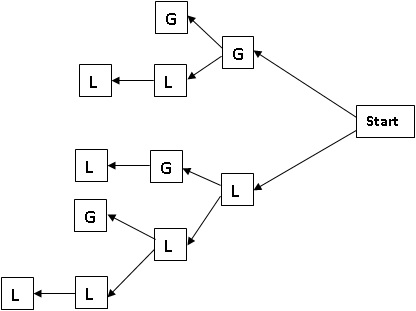
Figure 3
To generate the matra prastaar for a quarter having 5 matras (refer Table 4) I will draw the Tree graph given in Figure 4.
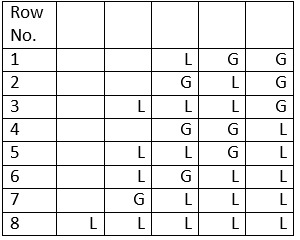
Table 4
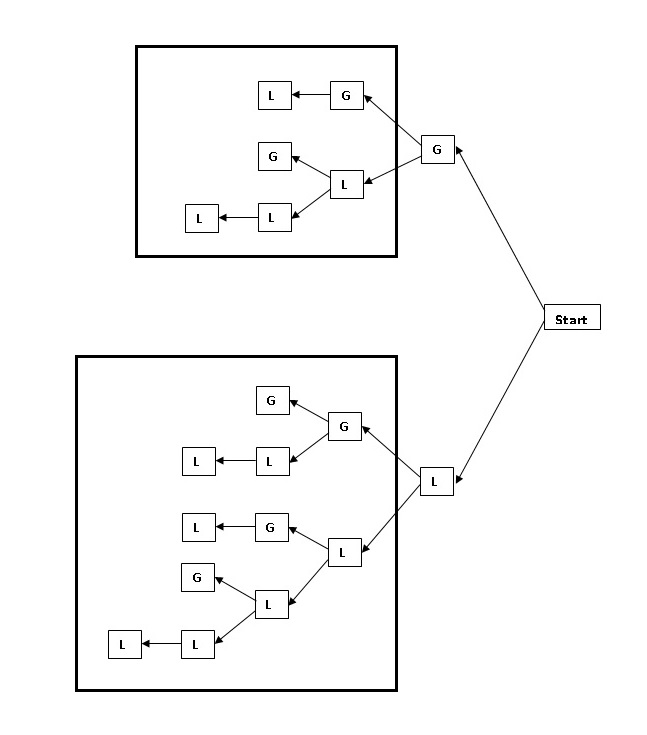
Figure 4
Refer Figure 4. The upper and lower rectangles give us the Tree graphs and matra prastaars for n = 3 and 4 respectively. Which shows us the recursive relation for the Sankhya pratyay.
It is clear from these tree graphs how Virahanka must have come up with the pratyay for matra prastaar.
Image Credit: Picxy.com/Aymen.noor
Disclaimer: The opinions expressed in this article belong to the author. Indic Today is neither responsible nor liable for the accuracy, completeness, suitability, or validity of any information in the article.