This is in continuation of my earlier article:
https://chandrahasblogs.wordpress.com/2020/04/22/how-pingala-created-the-binary-number-system/
In my earlier article I had explained how poetic meters of Sanskrit verses are classified based on the number of syllables (Laghu and Guru) and their arrangements in a quarter. Here we considered a fixed number of syllables in a quarter. This kind of classification is known as Varna vrutta (वर्ण वृत्त).
In this article I will discuss the classification of poetic meters based on the number of matras (मात्रा) (mora in English). This kind of classification is known as Matra vrutta (मात्रा वृत्त). Laghu (short) syllable is one matra in value (time period) and Guru (long) syllable is two matras in value (time period). In matra vrutta the quarter of a verse has fixed number of matras.
Pingala had only briefly touched upon Matra vrutta while discussing Arya and Vaitaliya meters. Matra vrutta is more common in Prakrit and regional languages. Virahanka (विरहाङ्क) (6th cent CE) gave a comprehensive explanation of the Prastaar and Sankhya pratyays for matra vrutta in his Prakrit work Vrattajati samuccaya (वृत्तजातिसमुच्चय:). A more detailed explanation of matra vruttas is given in Chandonusasana of Hemacandra (12th cent CE) and the books Prakrit Paingala and Vanibhusana (वाणीभूषणम्) by Damodara (15th cent CE).
How many poetic meters are possible for a quarter having n matras? Can you enlist all of them?
Virahanka had answered these questions. He had developed the Prastaar and Sankhya pratyay to enlist all the possible meters having n matras.
Virahanka’s Matra Prastaar
एष एव प्रस्तारो मात्रावृत्तानां साधितः किन्तु।
मात्रा यत्र न पूर्यते प्रथमं स्पर्शं तत्र देहि॥ – (वृत्तजातिसमुच्चयः ६.२०)
The procedure to generate the Matra Prastaar:
- The first row consists of all Gs if n is even and an L followed by all Gs if n is odd.
- Given any row in the prastaar, to generate the next row, scan from the left to identify the first G. Place an L below that. The elements to the right are brought down as they are.
- The remaining matras to the left are filled in by all Gs, and by placing an L at the beginning, if need be, to keep the total number of matras the same.
- The last row consists of all Ls.
The matra prastaar for a quarter having 1 matra:
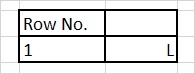
Table 1
Refer Table 1. The matra prastaar will have only one row, which will contain only a Laghu.
The matra prastaar for a quarter having 2 matras:
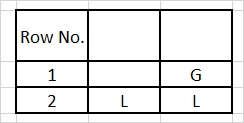
Table 2
Refer Table 2. The matra prastaar will have 2 rows. The first row will have a G and the second row will contain 2 Ls.
The matra prastaar for a quarter having 3 matras:
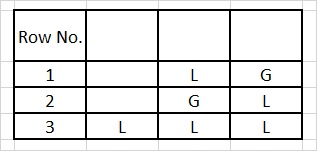
Table 3
Refer Table 3. Since n = 3 is an odd number the first row will contain a L at the beginning.
The matra prastaar for a quarter having 4 matras:
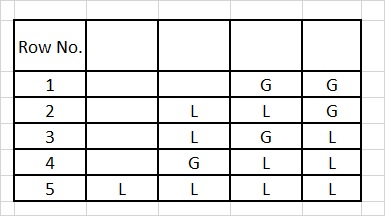
Table 4
Refer Table 4. Since n = 4 is an even number the first row will contain all Gs.
The matra prastaar for a quarter having 5 matras:
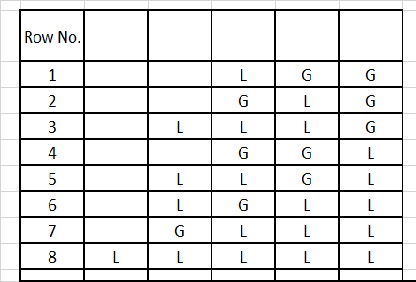
Table 5
Refer Table 5. Since n = 5 is an odd number the first row will contain an L at the beginning.
The matra prastaar for a quarter having 6 matras:
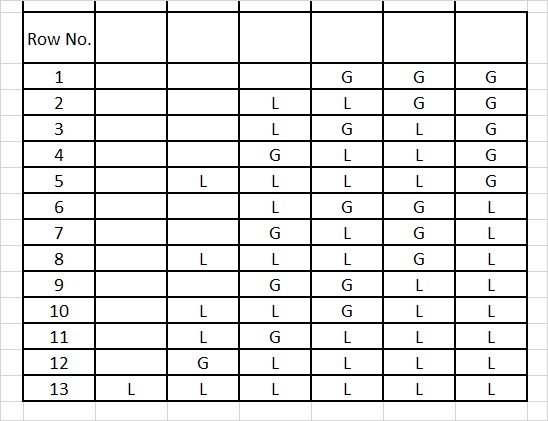
Table 6
Refer Table 6. Since n = 6 is an even number the first row will contain all Gs.
Now let us closely observe and analyse the prastaar for n = 6 matras.
The last column of the first 5 rows (row no.s 1 to 5) contains all Gs. As we know the value of G is 2. Then the matra values of the remaining columns of each of these rows needs to add up to 4. It means that the remaining columns of these rows should be the prastaar for n = 4. Refer Table 4, you will see that it exactly matches the prastaar for n = 4.
The last column of row no.s 6 to 13 contains all Ls. As we know the value of L is 1. Then the matra values of the remaining columns of each of these rows needs to add up to 5. It means that the remaining columns of these rows should be the prastaar for n = 5. Refer Table 5, you will see that it exactly matches the prastaar for n = 5.
Let Sn represent the number of all the possible poetic meters for a quarter having n matras or the number of rows in an n-matra prastaar. Then from the above discussion we have:
![]()
Let us consider a prastaar for a quarter having n matras. The rows in the prastaar end either with a G or an L. Now consider those rows that end with a G. Then the matra values of the remaining columns of each of these rows needs to add up to n-2. It means that the remaining columns of these rows should be the prastaar for n-2 matras. Now consider those rows that end with an L. Then the matra values of the remaining columns of each of these rows needs to add up to n-1. It means that the remaining columns of these rows should be the prastaar for n-1 matras.
Therefore, in general we can say that:
![]()
This was explained by Virahanka in his Sankhya pratyay given below:
द्वौ द्वौ पूर्वविकल्पौ या मेलयित्वा जायते सङ्ख्या।
सा उत्तरमात्राणां सङ्ख्याया एष निर्देशः॥ (वृत्तजातिसमुच्चयः ६.४९)
![]()
Then we get the following sequence of Virahanka’s Sankhyankas (सङ्ख्यांक)

As you might have already realised what is popularly known as Fibonacci sequence is actually the sequence of Virahanka’s Sankhyankas (सङ्ख्यांक).
In my next article I will explain how Virahanka may have come up with logic behind his Prastaar pratyay
Image Credit: flickr/Genista
Disclaimer: The opinions expressed in this article belong to the author. Indic Today is neither responsible nor liable for the accuracy, completeness, suitability, or validity of any information in the article.