This article is in continuation of my earlier articles published on Virahanka numbers: Part 1, Part 2, on Pingala’s binary number system and Pingala’s algorithm, Pingala’s Algorithm to find the value of a Binary Sequence

Let me present you one very amazing property of Virahanka’s numbers:
Any positive integer can be represented either as a Virahanka number or as a sum of non-consecutive Virahanka numbers (Sankhyaank), without repeating any of the number.
Let me demonstrate this with some examples:
38 = 34 + 3 + 1
77 = 55 + 21 + 1
23 = 21 + 2
94 = 89 + 5
Given a metrical form for a quarter having total matra value n can we find the row number for it in the matra prastaar for n matras?
Damodara used the above property and ingeniously developed the Uddishta (उद्दिष्ट) pratyay.
Let us say we have a row of 6 matras. Damodara had given each matra position a weightage / value sequentially equal to Virahanka numbers. Refer Table 2. A Laghu will occupy one matra position and a Guru will occupy two matra positions.

Damodara had given the below mentioned sutra in his book Vanibhusana for the Uddishta pratyay:
दत्वा पूर्वयुगाङ्कं गुरुशीर्षाङ्कं विलुप्य शेषाङ्के।
अङ्कैरितोऽवशिष्टैः शिष्टैरुद्दिष्टमुद्दिष्टम्॥ (वाणीभूषणम् १.३१)
Given a matra metrical form, from the left write down the sankhyaanks (Virahanka numbers) sequentially in the following ways:
1) For each G write two sankhyaanks, first above and the next below.
2) For each L, write one sankhyaank above.
3) Add all the sankhyaanks above the Gs. This sum subtracted from the total sankhyaanks (total number of rows) associated with the matra prastaar gives the row number.
Let me demonstrate this with some examples from a prastaar with n = 6.
Example 1
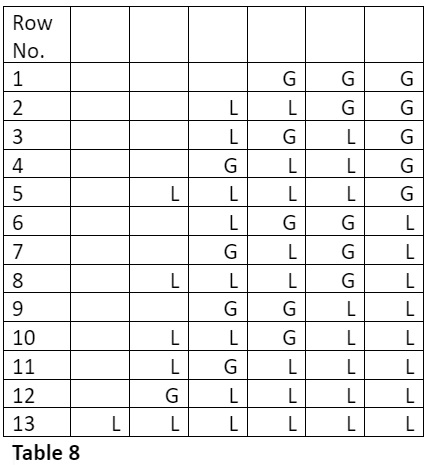
Find the row-number of the metrical form LGGL in the 6-Matra-prastaar.
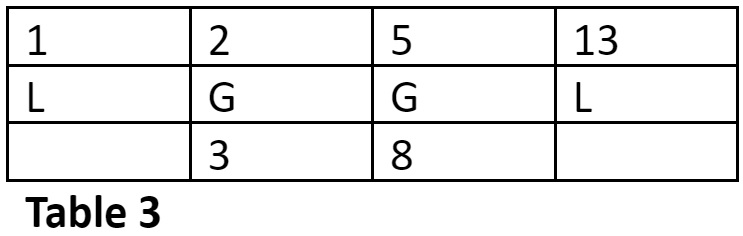
The row number is = 13 – (2 + 5) = 6
Example 2
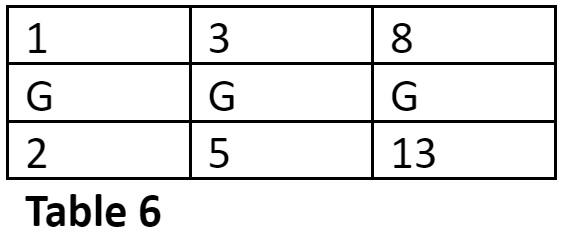
Find the row-number of the metrical form GGLL in the 6-Matra-prastaar.
The row number is = 13 – (1 + 3) = 9
Example 3
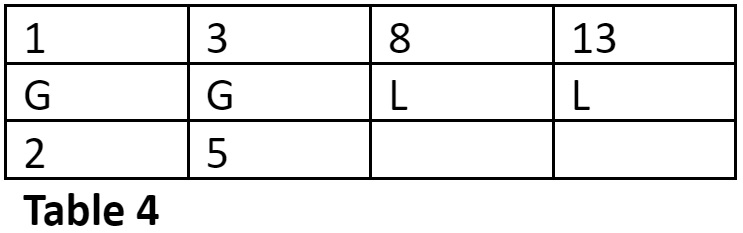
Find the row-number of the metrical form GLLLL in the 6-Matra-prastaar.
The row number is = 13 – (1) = 12
Example 4
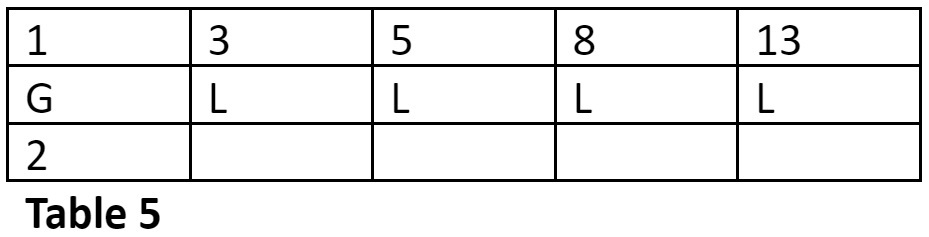
Find the row-number of the metrical form GGG in the 6-Matra-prastaar.
This is the first row in the 6-Matra-prastaar.
The row number is = 13 – (1 + 3 + 8) = 1
Example 5
Find the row-number of the metrical form LLLLLL in the 6-Matra-prastaar.
This is the last row in the 6-Matra-prastaar.
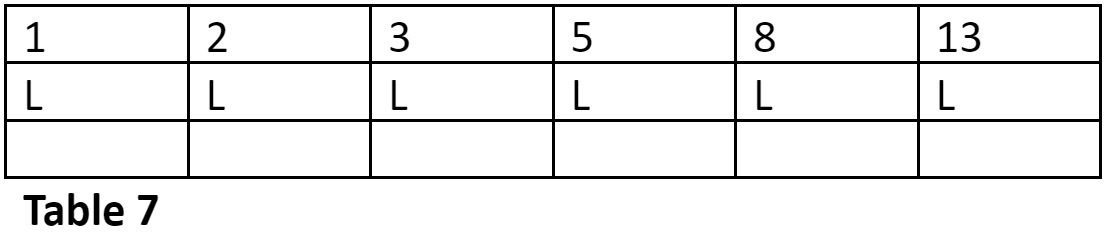
The row number is = 13
You can cross-check the answers with the 6-Matra-prastaar. Refer Table 8.
Now, given a row number in a n-Matra-prastaar can we find its metrical form?
Damodara had developed the Nashtam (नष्टम्) pratyay to achieve this. This is actually the converse of the Uddishta (उद्दिष्ट) pratyay.
Example 6
Let us understand this by finding the metrical form for the seventh row in the 6-matra-prastaar.
I should subtract 13 by 6 to get 7, the required row number. We have, 6 = 1 + 5. Hence, to get the metrical form for the seventh row we should place Gurus (Gs) at the matra position having weightages 1 and 5. Since a Guru occupies 2 positions, it will also occupy the succeeding position, as shown in Table 9. Of course the remaining positions will be occupied by the Ls.
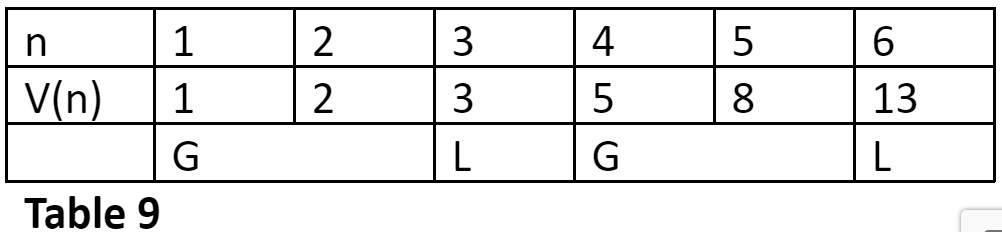
Thus, the metrical form for row 7 of the 6-matra-prastaar is GLGL. Cross check this answer with that in Table 8.
Now let me present the sutra for Nashtam pratyay given by Damadara in his book Vanibhusana:
नष्टे कृत्वा कलाः सर्वाः पूर्वयुग्माङ्कयोजिताः।
पृष्टाङ्कहीनशेषाङ्कं येन येनैव पूर्यते॥
परां कलामुपादाय तत्र तत्र गुरुर्भवेत्।
मात्राया नष्टमेतत्तु फणिराजेन भाषितम्॥ (वाणीभूषणम् १.३२-३३)
To find the matra metric form associated with a given row-number in the n-matra-prastaar:
- Write down n Ls with the sequence of sankhyaanks above them.
- Subtract the given row number from the sankhyaank Sn.
- From the result, subtract Sn – 1 if possible. Otherwise, subtract Sn – 2 and so on till the end.
- The matra metric form is obtained by converting each L below a sankhyaank which has been subtracted, together with the L to the right of it, into a G.
This is exactly what we had done in the above example. Let us now look at few more examples.
Example 7
Find the metrical form for the Third row in the 6-matra-prastaar.
I should subtract 13 by 10 to get 3, the required row number. We have, 10 = 2 + 8. Hence, to get the metrical form for the third row we should place Gurus (Gs) at the matra position having weightages 2 and 8. Refer Table 10.
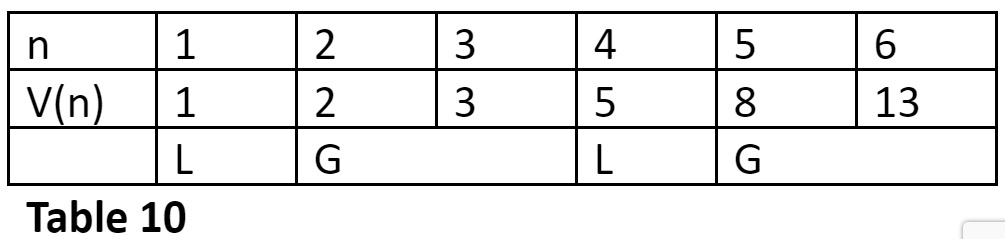
Thus, the metrical form for row 3 of the 6-matra-prastaar is LGLG.
Example 8
Find the metrical form for the twelfth row in the 6-matra-prastaar.
I should subtract 13 by 1 to get 12, the required row number. Hence, to get the metrical form for the twelfth row we should place a Guru (G) at the matra position having weightage 1. Refer Table 11.
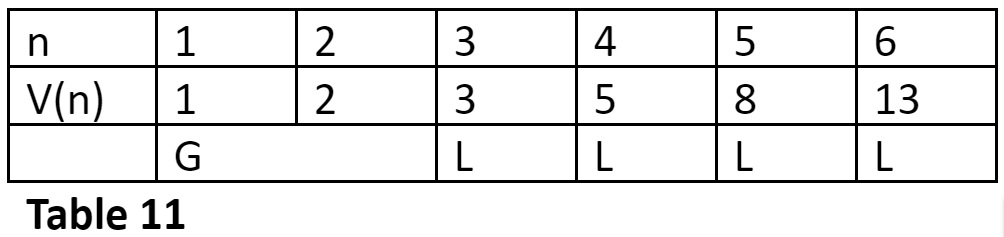
Thus, the metrical form for row 12 of the 6-matra-prastaar is GLLLL.
Image Credit: thedrum.com
Disclaimer: The opinions expressed in this article belong to the author. Indic Today is neither responsible nor liable for the accuracy, completeness, suitability, or validity of any information in the article.











