“Physically separated but digitally connected!” should be our motto in these days of the Coronavirus pandemic. Truly speaking digital technologies have enabled us to get through these days of lockdown.
Do you know, what is the fundamental principle on which today’s digital technology works? It is the binary number system.
But, do you know that this is the gift of ancient Indian mathematics to the world of technology. Ancient Indian prosodist and mathematician Pingala was the first to develop and use the binary number system while studying and analysing Sanskrit poetic meters (chandah / छन्द:) in his work Chandahshastra composed around 3rd century BCE.
The binary number system like the decimal number system is a place-value system. In the decimal number system, you have ten digits (0 and 1 through 9). Likewise in the binary number system, you have only two digits, 0 and 1, which are called bits. A bit is short for Binary digit.
The binary number system is a base two number system. In decimal number system the value of the digit depends on its position, i.e. digit times the power of ten. In the binary number system too, the value of the digit depends on its position, but here it is digit times the power of 2.
For example, the decimal number 237 is
237 = (2 x 100) + (3 x 10) + (7 x 1) = (2 x 10^2) + (3 x 10^1) + (7 x 10^0)
Binary equivalent of 237 is (1110 1101)2.
(1110 1101)2 = (1 x 2^7) + (1 x 2^6) + (1 x 2^5) + (0 x 2^4) + (1 x 2^3) + (1 x 2^2) + (0 x 2^1) + (1 x 2^0) = 128 + 64 + 32 + 0 + 8 + 4 + 0 + 1 = 237
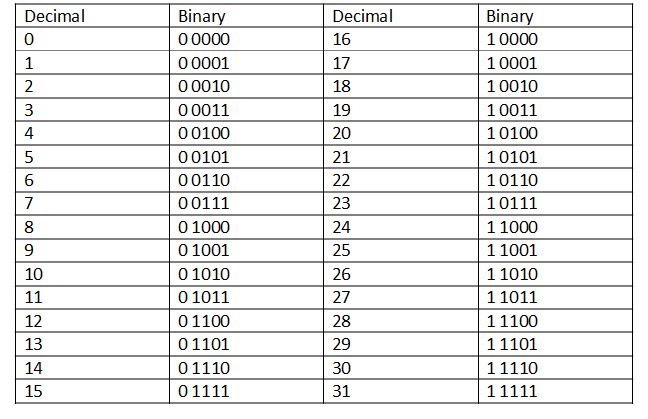
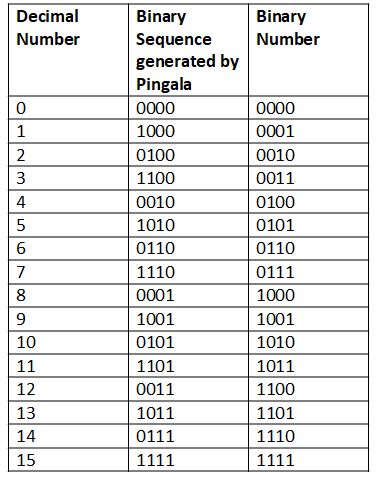
Table 1 gives you the binary equivalent of decimal numbers from 0 to 31. Kindly observe the pattern of the bits of the binary numbers in this table.
Table 1
You must now be wondering how Pingala developed a binary number system? To understand this let us first understand the basics of Sanskrit prosody.
Letters in Sanskrit can be either long (Guru / गुरु स्वर) or short (Laghu / लघु स्वर) syllables. These two types of syllables are the basic building blocks of Sanskrit prosody. A verse in classical Sanskrit literature has four quarters or pada (पाद) in a stanza. The metre of a verse is determined by the number of syllables and their order of arrangement in a quarter.
A syllable (अक्षर) is a vowel or a vowel with one or more consonants preceding it.
A short syllable is one ending with one of the short (hrasva / ह्रस्व ) vowels, which are a (अ), i (इ), u (उ), ṛ (ऋ) and ḷ (ऌ).
Even a short syllable will be a guru if what follows is a conjunct consonant, an anusvara or a visarga.
The long syllable is defined as one with one of the long (dirgha / दीर्घ) vowels, which are ā (आ), ī (ई), ū (ऊ), ṝ (ॠ), e (ए), ai (ऐ), o (ओ) and au (औ).
The last syllable of a foot of a metre is taken to be guru optionally.
Let us now understand Sanskrit metre with an example. Given below are the first two of a total of eight stanzas of Bhavani ashtakam (भवान्यष्टकम्), a beautiful composition by Adi Shankaracharya.
भवान्यष्टकम्
न तातो न माता न बन्धुर्न दाता
न पुत्रो न पुत्री न भृत्यो न भर्ता।
न जाया न विद्या न वृत्तिर्ममैव
गतिस्त्वं गतिस्त्वं त्वमेका भवानि ॥१॥
Neither father nor mother; neither the relative nor the benefactor,
Neither son nor daughter; neither servant nor husband,
Neither wife nor the (worldly) knowledge; nor Profession,
You alone are my refuge, you alone are my refuge, Oh Mother Bhavani.
भवाब्धावपारे महादुःखभीरु:
पपात प्रकामी प्रलोभी प्रमत्तः।
कुसंसारपाशप्रबद्धः सदाहं
गतिस्त्वं गतिस्त्वं त्वमेका भवानि ॥२॥
In the endless ocean of worldly existence, I am full of sorrow and much afraid,
I have fallen with excessive desires and greed, drunken and intoxicated,
Always tied in the bondage of this miserable samsara (worldly existence),
You alone are my refuge, you alone are my refuge, Oh Mother Bhavani.
Every quarter of Bhavani ashtakam consists of 12 letters. The pattern or the order of arrangement of syllables in each quarter is
LGG LGG LGG LGG
Here, G is Guru and L is Laghu syllable.
This metre is called भुजङ्गप्रयातम् (Bhujangaprayatam, snake-like advancing).
For a quarter having 12 letters, one can have 2^12 = 4096 different arrangements of Guru and Laghu syllables. This means that you can have 4096 different metres with a quarter consisting of 12 letters.
Pingala had developed technique (pratyay, प्रत्याय) or algorithm called Prastaar (प्रस्तार , meaning to unfold or to open up) for enlisting all the possible combinations of syllables for a quarter with length and letters.
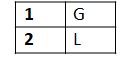
Table 2
For a metre having 2 syllables:
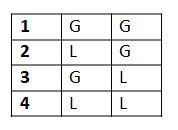
In step 1, Pingala copied the previous matrix immediately below itself. And in step 2, he filled up the upper half of the next column with 2 Gs and lower half with 2 Ls as shown in Table 3.
Table 3
For a metre having 3 syllables:
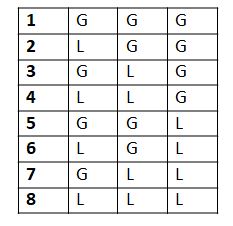
In step 1, Pingala copied the previous matrix immediately below itself. And in step 2, he filled up the upper half of the last column with 4 Gs and lower half with 4 Ls as shown in Table 4.
Table 4
For a metre having 4 syllables:
In step 1, Pingala copied the previous matrix immediately below itself. And in step 2, he filled up the upper half of the last column with 8 Gs and lower half with 8 Ls as shown in Table 5.
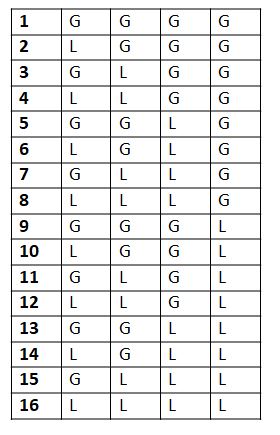
Table 5
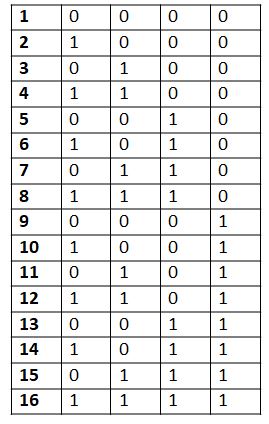
For metres with a larger number of letters, we can repeat this technique recursively. If we now replace G with 0 and L with 1 in Table 5, we get:
Table 6
If you compare Table 6 with Table 1 you will observe that the entries in Table 6 are mirror images of the binary equivalents of the numbers from 0 to 15. Refer to Table 7.
Table 7
This is how Pingala created the binary number system. This is one of the most significant contributions of India to the world of Mathematics.
To be continued…
Disclaimer: The opinions expressed in this article belong to the author. Indic Today is neither responsible nor liable for the accuracy, completeness, suitability, or validity of any information in the article.