Dimensions in Harappan Settlements
From the continuation of Part I, Ratios apart, we come across many dimensions of structures in Harappan settlements that can be expressed as integral multiples of our proposed Dholavira unit D = 1.9 m. A few examples are below in Table 4, while Fig. 7 illustrates the case of Mohenjo-Daro’s acropolis.
While every single dimension cannot be expected to be a whole multiple of D, it is striking enough that so many should turn out to be. This makes a strong case for Dholavira’s unit to have been one of the standards in the Harappan world, at least as far as town planning and architecture are concerned.
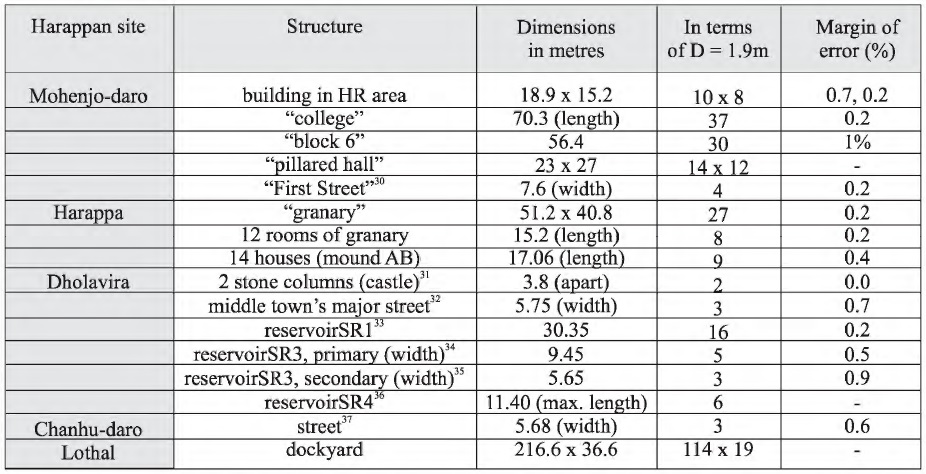
Table 4: Dimensions at various Harappan sites precisely expressed as integral multiples of D = 1.9 m. (The margin of error is included only if the published dimensions are judged precise enough).[i],[ii],[iii],[iv],[v],[vi],[vii], [viii]
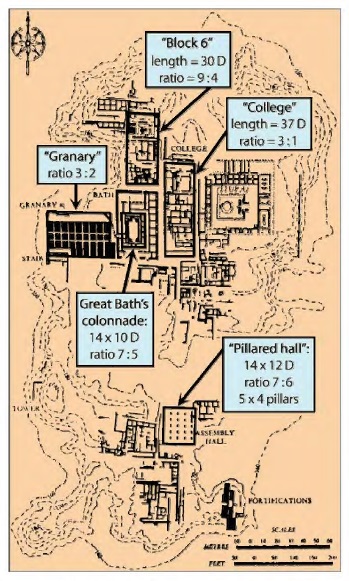
Fig. 7 Mohenjo-daro’s acropolis: a few ratios and dimensions expressed in terms of Dholavira’s unit D = 1.9 m.
Dholavira’s Dhanus and Angula
A unit does not exist singly: it is always part of a system. D = 1.9 m is a large unit and must have had subunits. In an attempt to figure them out, let us turn to divisions on the three known Harappan scales: those of Mohenjo-Daro (6.7056 mm), Harappa (9.34 mm),[ix] and Lothal (1.77 mm). The last is evidenced on an ivory scale found at Lothal, which has 27 graduations covering 46 mm. (Both S. R. Rao[x] and V.B. Mainkar erred in dividing 46mm by 27, when the length must of course be divided by the 26 divisions formed by the 27graduations).
Dividing D by the first two units yields no clear result. Dividing it by the Lothal unit (1904 by1. 77), we get 107 5. 7, or, with an approximation of 0.4%, 1080. This last number can be written 108 x 10.In other words, D can be expressed as 1 08 times 1. 77cm.
Let us pursue this line of inquiry: what is so special about 1.77 cm? First, let us remember that the values of the traditional digit in the ancient world, be it in Egypt, Mesopotamia, China, Greece, Japan or the Roman Empire, fluctuated between 1.6 and 1.9 cm.[xi] Ten times the Lothal unit falls in that range. Then, the Arthashastra defines a digit (angula in Sanskrit) as eight widths of barley grain (2.20.6) or “the maximum width of the middle part of the middle finger of a middling man” (2.20.7).[xii] Some eight centuries later, Varahamihira’s Brihat Samhita (LVIII.2) repeats the first definition; that is the “standard” angula of classical India (there are indeed variations in later or regional traditions of iconometry, but they need not detain us here). Most scholars from J.F. Fleet down took the angula to be “roughly 3/4th of an inch”,[xiii] that is, 1.9 cm. K.S. Shukla,[xiv] Ajay Mitra Shastri[xv] or A.K. Bag,[xvi] to quote just a few, endorsed this approximate value. In contrast, the metrologist V.B. Mainkar[xvii] traced the “development of length and area measures in India” and narrowed the value of the angula to 17.78 mm. He was probably the first to suggest that 10 times the Lothal unit, i.e. 1. 77 cm, was almost identical to the traditional angula.
Moreover, a crude terracotta scale from Kalibangan was submitted to careful scrutiny by the late R.Balasubramaniam, who established that it is based on a unit of 1.75 cm.[xviii] This is almost the same as the Lothal unit of 1. 77 cm.
Let us average the two and call 1.76 cm “A” for angula; we then have the following relation: D = 108A. This is an arresting result, since the concept of”108angulas” is well attested in classical India. For instance, one of the systems of units described in Kautilya’s Arthashastra (2.20.19) fits very well in the Dholavirian scheme: “108 angulas make a dhanus (meaning a bow), a measure [used] for roads and city walls.”[xix] “City walls” is precisely the context in which our unit D was used at Dholavira and elsewhere. We can now propose that “D” also stands for dhanus.
The Harappan brick provides us with a degree of confirmation of the Lothal angula. In the Mature phase (and occasionally in the Early phase), most bricks follow ratios of 1:2:4 in terms of height width-length; among several different sizes in this ratio, one dominates by far: 7x 14 x 28 cm, measured and averaged over numerous samples (as mentioned by Kenoyer[xx] and by Rottlander quoting Jansen[xxi]); the first dimension, 7 cm, is almost exactly 4 Lothal angulas (the difference being just0.5 mm or 0.7%). So the humble brick’s dimensions can be elegantly expressed as 4 x 8 x 16A.
Between the angula and the dhanus, there must have been several important subunits, and elsewhere[xxii] I attempted to work out a few of them; preliminary findings are that units of 4, 8, 10, 15, 16, 27 and 36angulas were probably in use in Harappan times. However, this requires confirmation through more systematic studies.
Continuity of the Dholavira Scheme of Ratios and Units
The scheme of ratio and units found at Dholavira finds further echoes in historical times. The Arthashastra apart, “many [early texts] concentrate on the description of an image of 108 angulas in length.”[xxiii] The origin of the concept behind the sacred number 108 is probably multiple. It could be simply based on the human body: 108 angulas (1.9m) is the height of a tall man, as specifically mentioned by Varahamihira in his Brihat Samhita (68.1 05).[xxiv] From a different perspective, simple but compelling astronomical considerations behind 108have been demonstrated by Sub hash Kak.[xxv]
Dholavira’s ratios must have been perceived as especially auspicious, otherwise every enclosure might as well have been square. Some of those ratios are still in use in various traditions of Vastu Shilpa. In the sixth century CE, for instance, Varahamihira wrote in his Brihat Samhita (53.4 &5):
The length of a king’s palace is greater than the breadth by a quarter…. The length of the house of a commander-in-chief exceeds the width by a sixth.[xxvi]
These two ratios, 1 + 1/4 and 1 + 1/6, are identical to5:4 and 7:6 – very precisely Dholavira’s most prominent ratios (see Fig. 2). Such a perfect double match appears to be beyond the realm of coincidence.
A recent work by Mohan Pant and Shuji Funo[xxvii] compared the grid dimensions of building clusters and quarter blocks of three cities: Mohenjo-Daro, Sirkap (Taxila, early historical, Fig. 8), and Thimi (in Kathmandu Valley, a contemporary town of historical origins). Carefully superimposing grids on published plans of all three cities (their own in the case of Thimi), the authors found that block dimensions measure 9.6 m, 19.2 m (= 9.6 m x 2), or multiples of such dimensions. This, they argue,
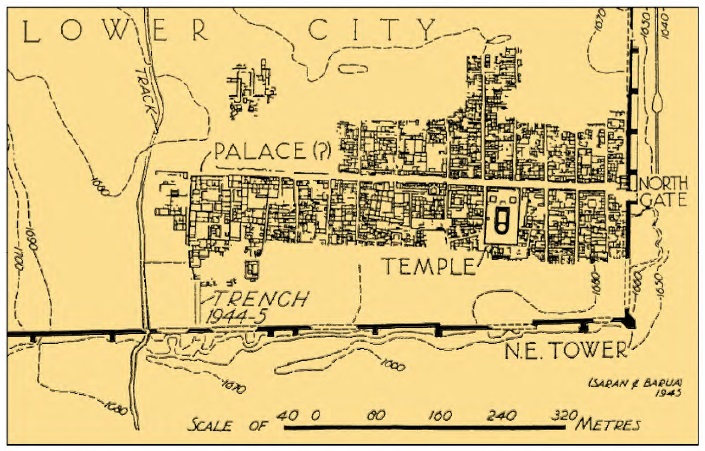
Fig. 8: Plan of Sirkap, one of Taxila’s mounds. The blocks of houses are separated by regularly spaced streets, 38.4m apart (=1.92×20).
evokes the Arthashastra’s unit called rajju, equal to 10 dandas. As regards the danda, which has four possible traditional values, the authors choose that of 108 angulas as prescribed in the Arthashastra (2.20.18-19); it is the same passage which I quoted earlier to define the dhanus, and the danda is mentioned in it as another name of the dhanus: for our purposes, the two terms are identical.
Pant’s and Funo’s unit of 1.92 m differs from mine of1.9 m by just 1%; in both cases, the unit was equated108 angulas. Their work thus lends support to my suggestion that such concepts survived the collapse of Harappan urbanism and re-emerged in Kautilya’s canons of urbanism. Is this so surprising, when we already know that the Harappans’ weight system, metallurgical, agricultural and craft techniques did live on, apart from numerous religious symbols and practices?[xxviii]
We get further confirmation of such continuity from a case study of the Delhi Iron Pillar (Qutub Minar complex) by R. Balasubramaniam,[xxix] who applied to it the Harappan dhanus and angula I had proposed and found they expressed the pillar’s dimensions with unexpected harmony (Fig. 9): its total length of7. 67 m, for instance, is precisely 4 D; its diameter, 36 angula sat the bottom, shrinks to 24 angulas at ground level, finally to taper off at 12 angulas at the very top. If this were not enough, the ratio between the pillar’s entire length (7.67 m) and the portion above the ground (6.12m) is 5:4, verified to 0.2% – again, Dholavira’s master ratio. This bears out once again that Harappan ratios and linear units survived the collapse of the Indus cities and passed to those of the Ganges Valley. Balasubramaniam applied the same units with excellent results to engineered caves of the Mauryan period[xxx] and to the Taj Mahal complex,[xxxi] opening a newline of inquiry in classical Indian metrology.
Harappan and Classical Concepts
On a cultural level, the presence of carefully proportioned fortifications as at Dholavira might be as much a specific cultural trait as pyramids are to Egypt or ziggurats to Mesopotamia. Here, instead of erecting colossal buildings, enormous energy was spent on defining spaces: the space of the rulers and administrators (the acropolis) and the spaces for other classes of citizens. Demarcating was a vital need not for defense, but for self-definition: fortifications probably stood for authority and segregation, as Piotr A. Eltsov has recently argued too. [xxxii]
But there may also be deeper motives at work: ratios and units apart, we can discern a few important
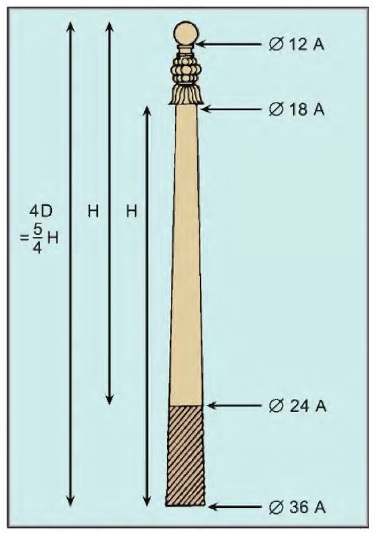
Fig. 9: A sketch on the Delhi Iron Pillar with the main dimensions expressed in terms of D = Dholavira’s dhanus (1.9 m) and A= Dholavira’s angula (1.76
principles underlying Dholavira’s fascinating harmony, in an almost Pythagorean sense of the term. More work and data are needed to bring out those principles securely, but I proposed elsewhere[xxxiii] that the Vedic principle of addition of a unit is at work here: 5:4 should be read as “one unit plus one fourth”, and the key ratio of 9:4, for instance, is nothing but 5:4 plus one unit. This addition to the unit of a fraction of itself can also be seen as a process of expansion, of auspicious increase symbolizing or inviting prosperity. Thus the Manasara, a treatise of Hindu architecture, applies this process when it specifies (35.18-20) that ”the length of the mansion [to be built] should be ascertained by commencing with its breadth, or increasing it by one-fourth, one-half, three fourth, or making it twice, or greater than twice by one fourth, one-half or three-fourths, or making it three times.”[xxxiv] The outcome is a series of ratios: 5:4, 3:2, 7:4, 2:1, 9:4, 5:2, 11:4, 3:1. Since we found all these ratios at Dholavira or other Harappan settlements, it is tempting to assume that the concept behind such auspicious ratios was the same in Harappan times.
Also found at Dholavira is another Vedic principle, that of recursion or repetition of a motif. [xxxv]Thus the “castle” and the overall city share the same ratio (5:4), and 9:4 defines the expansion from the length of the “castle” to that of the middle town, and again to that of the lower town.
The thread connecting those principles was anticipated by astrophysicist J. McKim Malville, who saw in Dholavira’s features “the apparent intent … to interweave, by means of geometry, the microcosm and the macrocosm”.[xxxvi] To the ancient mind, the concept of sacred space was inseparable from the practice of town-planning and architecture. Dilip Chakrabarti echoes this in his recent observation: “The ideals of ancient Indian town planning seem to run deep through the concepts embedded in the Harappan cities like Mohenjo-Daro.
References
[i] Gregory L. Possehl, The Indus Civilization: A Contemporary Perspective, op. cit., p. 101.
[ii] B.B. Lal, India 1947-1997: New Light on the Indus Civilization, op. cit., p. 44.
[iii] Ibid.
[iv] Michel Danino, “Further Research into Harappan Metrology at Dholavira”, op. cit.
[v] Ibid.
[vi] Ibid.
[vii] Ibid.
[viii] Dilip K. Chakrabarti, The Oxford Companion to Indian Archaeology, op. cit., p. 154.
[ix] V. B. Mainkar, “Metrology in the Indus Civilization”, op.cit., p.l46.
[x] S. R. Rao, Lothal, a Harappan Port Town (1955-62), Archaeological Survey of India, New Delhi, 1979, vol. 2, p. 626.
[xi] R.C.A. Rottlander, “The Harappan Line Measurement Unit”, Reports on Field Work Carried out at Mohenjo-Daro: Interim Reports Vol. 1, M. Jansen and G. Urban, eds., German Research Project Mohenjo-Daro RWTH Aachen, Aachen, 1983, p.205.
[xii] R. P. Kangle, The Kautilya Arthasastra, Motilal Banarsidass, New Delhi, 1986,partii,p.138.
[xiii] Debiprasad Chattopadhyaya, History of Science and Technology in Ancient India: The Beginnings, FirmaKLM, Calcutta 1986, p. 231.
[xiv] Kripa Shankar Shukla, Aryabhatiya of Aryabhata: Indian National Science Academy, New Delhi 1976, p. 19.
[xv] Ajay Mitra Shastri, Ancient Indian Heritage: Varahamihira’s India, Aryan Books International, New Delhi, 1996, vol. II, p. 327.
[xvi] A.K. Bag, History of Technology in India, Indian National Science Academy, New Delhi, 1997, vol. I, p. 667.
[xvii] V. B. Mainkar, “Metrology in the Indus Civilization”, op. cit., p. 147.
[xviii] R. Balasubramaniam & Jagat Pati Joshi, “Analysis of terracotta scale of Harappan civilization from Kalibangan”, Current Science, vol. 95, no. 5, 10 September 2008, pp. 588-89.
[xix] R.P. Kangle, The Kautilya Arthasastra, op. cit., p. 139.
[xx] Jonathan Mark Kenoyer, Ancient Cities of the Indus Valley Civilization, op. cit., p. 57.
[xxi] R.C.A Rotlander, “The Harappan Linear Measurement Unit”, op. cit., p. 202.
[xxii] Michel Danino, “New Insights into Harappan Town-Planning, Proportions and Units, with Special Reference to Dholavira”, Man and Environment, vol. XXXIII, no. 1, 2008, pp. 66-79.
[xxiii] Isabella Nardi, “On Measuring Images: a Critical Analysis of the Theory of Talamana”, Sahrdaya: Studies in Indian and South East Asian Art in Honour of Dr. R. Nagaswamy, Bettina Baumer, R.N. Misra, Chirapat Prapandvidya & Devendra Handa, eds., Tamil Arts Academy, 2006, Chennai, p.260.
[xxiv] M. Ramakrishna Bhat, Varahamihira’s Brihat Samhita, Motilal Banarsidass, New Delhi, 1981, vol. l,p. 642.
[xxv] Subhash Kak, The Astronomical Code of the Rigveda, Munshiram Manoharlal, New Delhi, 2nd ed., 2000, pp.101-02& 124.
[xxvi] M. Ramakrishna Bhat, Varahamihira’s Brihat Samhita, op. cit., pp. 451-52.
[xxvii] Mohan Pant & Shuji Funo, “The Grid and Modular Measures in the Town Planning of Mohenjo-Daro and Kathmandu Valley: A Study on Modular Measures in Block and Plot Divisions in the Planning of Mohenjo-Daro and Sirkap (Pakistan), and Thimi (Kathmandu Valley)”, Journal of Asian Architecture and Building Engineering, 2005, 4(1), pp. 51-59, retrieved from: www.j stage.jst.go.jp/article/jaabe/4/1 /51/ _pdf on09.09.07.
[xxviii] Michel Danino, “The Harappan Heritage and the Aryan Problem”, Man and Environment, 2003, X: XVIII (1): 21-32.
[xxix] R. Balasubramaniam, “On the mathematical significance of the dimensions of the Delhi Iron Pillar”, Current Science, vol. 95, no. 6, 25 September2008, pp. 766-70.
[xxx] R. Balasubramaniam, ”New insights on metrology during the Mauryan period”, Current Science, vol. 97, no. 5, 10 September 2009, pp. 680-82.
[xxxi] R. Balasubramaniam, ”New insights on the modular planning of the Taj Mahal”, Current Science, vol. 97, no.1, 10July2009, pp. 42-49.
[xxxii] Piotr A. Eltsov, From Harappa to Hastinapura: A Study of the Earliest South Asian City and Civilization, Brill Academic Publishers, Boston, Lei den, 2007.
[xxxiii] Michel Danino, “New Insights into Harappan Town-Planning, Proportions and Units, with Special Reference to Dholavira”, op. cit.
[xxxiv] Prasanna Kumar Acharya, Architecture of Manasara (vol. IV in Manasara Series), 1934, republished Munshiram Manoharlal, New Delhi, 1994, p.374.
[xxxv] Subhash Kak, “Archaeoastronomy in India”, online at http:/ /arxiv.org/pdf/1 002.4513v1 (retrieved23.12.201 0).
[xxxvi] J. McKim Malville & Lalit M. Gujral, eds., Ancient Cities, Sacred Skies: Cosmic Geometries and City Planning in Ancient India, Indira Gandhi National Centre for the Arts & Aryan Books International, New Delhi,2000,p. 3.
This article was first published in Propagation: A Journal of Science Communication and has been republished with the permission of the author.
(This article was published by IndiaFacts in 2018)
Disclaimer: The opinions expressed in this article belong to the author. Indic Today is neither responsible nor liable for the accuracy, completeness, suitability, or validity of any information in the article.










