The vast corpus of traditional knowledge accessible to us today had flourished for centuries as the spoken word. Right from the Vedic literature, upon which the Indic thought firmly rests, the roots of the oral tradition go wide and deep. Even when knowledge was written down, it was often terse, with a lot of ideas and subject areas discussed in condensed forms, leaving ample scope for commentaries and explanatory notes. Bhashyas are a common feature of the Indic tradition.
Some historians attribute the oral tradition to the exclusivity of knowledge. This is far from the truth. Educational systems in ancient India were all-embracing, holding no difference between nobles and commoners [1]. Knowledge was seldom kept hidden. Instead, the oral tradition was given importance because it placed great emphasis on the purity of sound. After all, it is sound that breathes meaning into a word. Pronunciation and proper memorization were deemed as important as writing to preserve the true meaning of anything. This is especially so in Sanskrit and Indic languages where the acoustic roots of a word (dhwani), and its meaning are intimately intertwined.
This approach to preservation and transmission of knowledge through speech was so conventional that ideas in many fields were expressed in a similar way that it could be remembered and recollected without having to rely on the written material. The practice led to two main systems of codifying information – the akshara-samkhya, and bhuta-samkhya. In the former system, numbers were mapped to letters of the Sanskrit alphabet, and in the latter, they were mapped to objects, or specific words [2]. In this essay, we focus on the akshara-samkhya system, which is also popularly known as katapayadi.
The KaTaPaYadi is a system of concealing numbers by encoding them into alphabets. It was a kind of simple cryptography, though the purpose was not to keep the knowledge concealed. Rather, it provided a convenient way to remember unique numbers, values of mathematical functions, numerical formulae, constants used in mathematical computations, dates corresponding to events, and so on by embedding them into prose or poetry. The rules are simple, and the decoding straightforward.
The exact origin of this system is unknown. Many attribute it to Vararuci, a brilliant scholar from Kerala of the fourth century CE. The chandra-vakhyas, authored by Vararuci, is a collection of sentences in Sanskrit used for computing lunar positions. In chandra-vakhyas we have one of the oldest written pieces of evidence where the katapayadi scheme is used [2]. On that account, the origins of katapayadi is also traced back to Vararuci.
The dating of chandra-vakhyas is an unsettled issue. There are clear indications that scholars later to Vararuci, such as Aryabhata I (5th century CE), and Haridatta (7th century CE), were well aware of the katapayadi scheme [3]. One also finds extensive use of katapayadi in the mathematics and astronomy works of the long tradition of scholars from Madhava to Sankara Varman who lived in Kerala from the 14th to 18th century CE. Their written works firmly establish the extensive use of katapayadi in Kerala.
In Malayalam, the regional language of Kerala, katapayadi is also known as പരൽപ്പേര് (paral-peru). The word “paral” in Malayalam has a reference to the sea. In a practice followed in predictive astrology of Kerala, even today, tiny seashells are used as a counting frame for computing planetary configurations, much like an abacus (see photograph below). The calculations are done by remembering verses whose numerical meanings are encoded using katapayadi. This is most likely why katapayadi was known locally in Kerala as paral-peru [3].
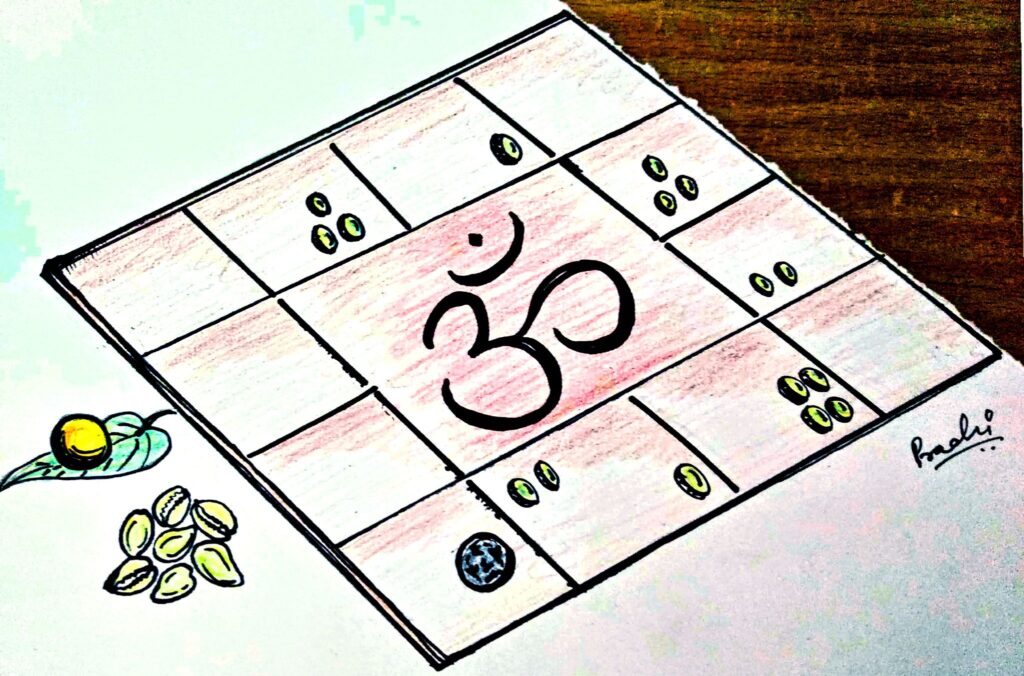 In predictive astrology as practiced in Kerala even to this day, tiny seashells (called kavadi) are used to depict the position of planets at different times. Illustration by Prachi Prajapati
In predictive astrology as practiced in Kerala even to this day, tiny seashells (called kavadi) are used to depict the position of planets at different times. Illustration by Prachi Prajapati
The Katapayadi Scheme – Many to One Mapping
Katapayadi uses Sanskrit consonants to represent numbers of the decimal system. Thus, the first consonant क (‘Ka’) is assigned the numerical value 1. The second consonant ख (‘Kha’) is assigned the value 2, and so on, till one gets to ज (‘jha’) which is represented by 9 and ञ (‘Nja’) by 0

The numbers are then assigned similarly to the next set of ten consonants. In this scheme, we therefore end up having multiple alphabets representing the same number. The number ‘1’ is mapped to the alphabets Ka, Ta, Pa, and Ya, which when put together gives KaTaPaYa-adi, where adi means etcetera.
The vowels or swara aksharas are not assigned any numerical value. So for example, क, का, के, कै, को, कौ, कि, and की would all represent the number 1. This basic approach of mapping numbers to letters is summarized in the following verse from sadratnamala, a text written by the 18th-century mathematician Sankara Varman

The first sentence says that “all vowels such as na and njya carry a value of sunya or zero”, “the nine integers (from 1 to 9) are represented by the consonant group beginning with ka, ta, pa, and ya”. The second sentence reads “in a misram (where two consonants are conjoined), only the second consonant should be taken into consideration, and that “a consonant in half form should be ignored altogether”. An example of a misram would be ज्य, wherein the katapayadi scheme of decoding ज is ignored, and य is considered. Examples of consonants in half forms are त् , न् , म् etc, which are half forms of त, न, म . These are ignored altogether.
The decoding of a sentence follows the rule अङ्कानां वामतो गतिः (anganam vamatho gathi), which says that the numbers move in their place value from left to right. In other words, the number obtained from decoding a katapayadi word or a sentence has to be read from right to left. For example, the number Two Thousand Five Hundred and Thirty-Nine will be written in katapayadi as 9352 but has to be read, reversing the order from right to left, as 2539. With these basic rules in mind, let us now look at some famous examples of katapayadi encryption.
We have created a short video tutorial on katapayadi that offers an overview of the topic. In the essay, we venture deeper into the details.
Tabulations of Sine Value & the Infinite Series for Sine
Much of mathematics in India was developed as a tool for astronomical calculations that went into the design of calendars to reckon time. It is most easy to refer to positions of objects in the sky in terms of angles measured against a common reference point. Consequently, trigonometric functions of angles such as sinθ, and cosθ were used for calculating the separation between objects in the sky, their position with reference to the horizon, and the path they trace in the sky with time. Since the sky appears as a hemisphere for any observer on Earth, these trigonometric functions were often defined in terms of arc segments of a circle.
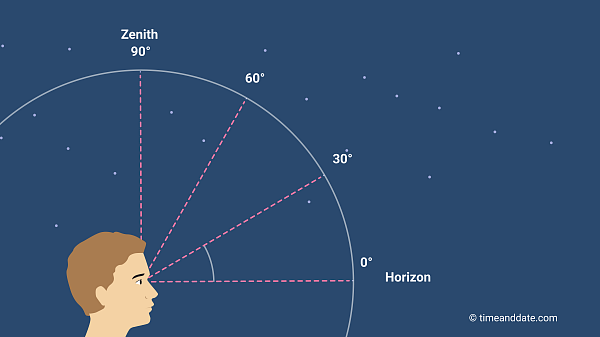 The drawing shows how locations of stars in the sky can be marked using angles with reference to some point, say the horizon. ©timeanddate.com
The drawing shows how locations of stars in the sky can be marked using angles with reference to some point, say the horizon. ©timeanddate.com
An arc is nothing but a curve, a portion of a circle. If there is a circle of radius R, then the arc lengths corresponding to the different values of the angle θ (pronounced, theta) are given by R sinθ (refer to figure below). To be exact, R sinθ is the linear approximation of the arc length. But when the arc length is small, this turns out to be a fairly good approximation.
The arc length Rsinθ, often written as Rsine, is referred to in the ancient mathematical texts as jya or jiva. The figure below illustrates what a jya is, and how it relates to the arc length (also called chapa).
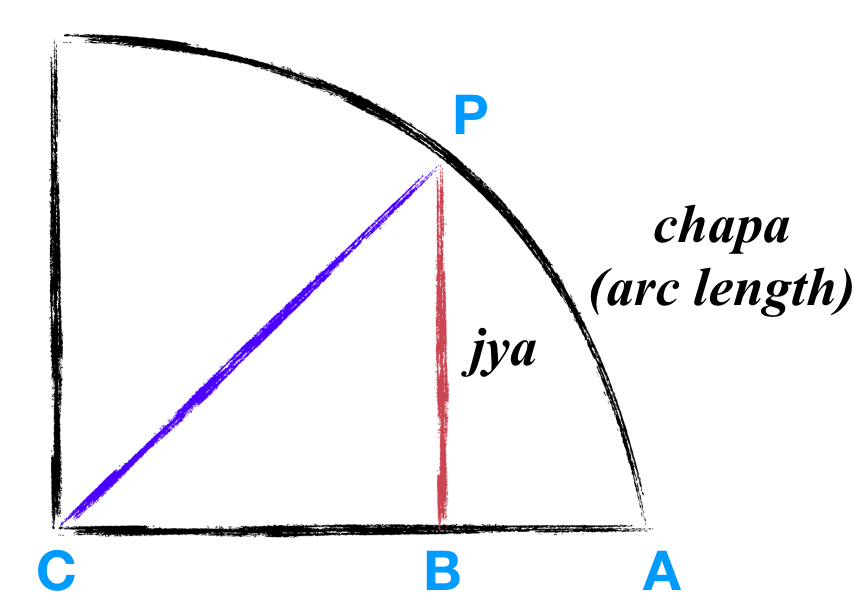 Figure shows quarter of a circle. AP is an arc, also called chapa (meaning “bow”). BP is the Rsinθ (or Rsine) corresponding to that arc AP. Here θ is the angle between the lines AC and CP, and R is the radius of the circle which is equal to CP. The Rsine is called jya or jiva, and is a linear approximation of the length of the arc AP.
Figure shows quarter of a circle. AP is an arc, also called chapa (meaning “bow”). BP is the Rsinθ (or Rsine) corresponding to that arc AP. Here θ is the angle between the lines AC and CP, and R is the radius of the circle which is equal to CP. The Rsine is called jya or jiva, and is a linear approximation of the length of the arc AP.
Methods to arrive at the Rsine values for any angle are given in several texts including Aryabhata’s aryabhatiya (5th century CE), Varahamihira’s pancasiddhantika (6th century CE), Bhaskara’s mahabhaskariya (7th century CE), Nilakanta Somayaji’s tantrasangraha (15th century CE), and Sankara Variyar’s yuktidipika (16th century CE), which incidentally is a commentary on tantrasangraha. In the latter two works, the idea presented is attributed to Madhava (14th century CE), who was a predecessor to Nilakanta Somayaji and Sankara Variyar.
In yuktidipika one finds an interesting use of katapayadi in the tabulation of the values of Rsinθ for sequentially increasing range of angles from zero to ninety degrees. The verse goes as follows [6] :

If we take a quarter of a circle and slice it up into 24 equal size wedges each wedge will be 3.75 degrees in angular size as shown in the illustration below.
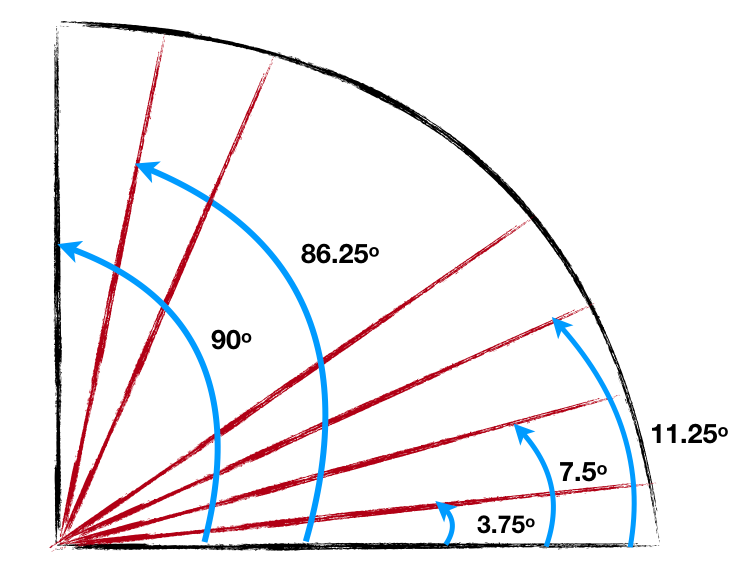 A quarter of a circle is sliced into 24 wedges of equal size. Each wedge will have an angular size of 3.75 degrees. The small angles are exaggerated a bit in the diagram for illustrative purposes
A quarter of a circle is sliced into 24 wedges of equal size. Each wedge will have an angular size of 3.75 degrees. The small angles are exaggerated a bit in the diagram for illustrative purposes
Words from the above verse, when decoded using katapayadi, gives the jya value (i.e, the Rsinθ value) for uniformly increasing angles from 0 to 90 degrees in steps of 3.75 degree. From that, the corresponding sin θ values can be easily estimated. A detailed description of this is given in Appendix – I.
Madhava could not have articulated the values for the sine function to such an exact level of accuracy (see Appendix I) without access to a mathematical expression. Indeed, yuktidipika gives a general expression for sinθ for any value of the angle θ as a sum of an infinite number of terms. Yuktidipika, once again, attributes this expression to Madhava [4]. The expression in modern notation can be written as –
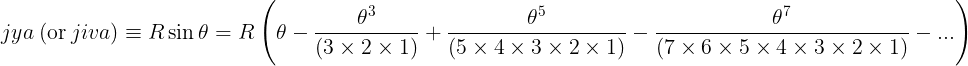
In the history that is taught to us, the above series expansion extending to an infinite number of terms is credited to Brook Taylor (1685 – 1731). In contemporary mathematics, we refer to it as the Taylor series. It appears in a work that he published in 1715. Variants of this series are featured in the works of Issac Newton (1642 – 1727), Gottfried Wilhelm Leibniz (1646 – 1716), Leonard Euler (1707 – 1783), and a few others.
In the above series expression, each successive term that is added or subtracted has progressively diminishing values because of the increasing denominator. Expressing an entity with a definite value (such as the sine of an angle) in terms of an algebraic expression involving the sum of an infinite number of such terms of diminishing numerical value is one of the foundations of modern calculus. Indeed, calculus is often spoken about as the mathematics of infinitesimals.
Madhava invented these power series expansions of trigonometric functions three centuries prior to Taylor. It was documented by a number of native scholars who succeeded him, a lineage which modern historians refer to as the Kerala School of Mathematics and Astronomy. In his book A Passage to Infinity, the mathematician George Gheverghese Joseph makes a strong case for possible transmission of the mathematical knowledge of the Kerala school to Europe through Jesuit priests and trade travelers who took to the sea, frequenting the southwest coast of India from 1540 CE onward (see chapter 9 of that book).
The Naming of Ragas
A really interesting application of katapayadi is in the naming of raga in Indian classical music. From the wide range of melodic scales that are part of the South Indian classical music system, there are 72 ragas that are unique in that they contain all the seven notes of the octave (sapta swaras) in the ascending (arohanam) and descending scales (avarohanam). These 72 ragas are called melakartha, or sampoorna ragas (‘complete ragas’ as they carry all seven swaras). The melakartha can be regarded as the parent ragas, janaka ragas, from which many other melodic scales, called janya ragas, are derived by dropping one or more notes or rearranging the sequence in which the notes appear in the ascending and descending scales.
First propounded in the mid 15th century CE by Raamamaatya, the mēḷa system of arranging ragas got revised and refined over two centuries. The sequence of 72 mela ragas, as followed now, was expounded by Venkatamakhin in the text catur-dandi-prakasika, written during the 17th century CE [5]. However, there is no evidence that Venkatamakhin had given unique names to the 72 ragas using the katapayadi scheme. That seems to have happened much later [5].
The melakarta system uses katapayadi to name the ragas. Before explaining this further, let us briefly go through a few basics on swaras and their unique formations that lead to specific ragas.
There are seven basic swaras in music, which completes one full octave.
सा (Sa) री (Ri) ग (Ga) म (Ma) प (Pa) ध (Dha) नि (Ni)
The swaras are arranged in increasing order of frequency from left to right (i.e., from Sa to Ni). Among these, the two swaras Sa and Pa have no frequency variants, but the other five notes have slightly different frequency variants, often called ‘semitones”. These variants are typically notated in short form as:
S, R1,R2, R3, G1,G2, G3, M1,M2, P, D1,D2, D3, N1,N2, N3
It is the different combinations of these notes and the variants of the notes that gives form to the 72 melakartha ragas. The distinctive feature of melakartha ragas is that each of them will have seven basic notes in both the ascending and descending scales. No note will be skipped. Every melakartha raga will have Sa and Pa. They will also have either one from the two variant notes of Ma, and one from the three variant notes for Ri, Ga, Dha, and Ni.
The 72 melakartha ragas can be divided into two groups of 36 each. In the first set of 36 ragas, the following notes are fixed in the arohanam and avarohanam S _ _ M1 P _ _ S, and in the second set, the following notes are fixed S _ _ M2 P _ _ S.
In the vacant positions, indicated by “ _ “, one has the option to fill the variants of the remaining swaras Ri, Ga, Dha, and Ni. Here again, while going on an ascending scale, only six mutual combinations of Ri and Ga, and six combinations of Dha and Ni are possible. These are:
R1 – G1, R1 – G2, R1 – G3 |
R2 – G2, R2 – G3 |
R3 – G3 |
D1 – N1, D1 – N2, D1 – N3 |
D2 – N2, D2 – N3 |
D3 – N3 |
Which combinations of these go into filling the swara sequence determines the raga. Each of the 6 combinations of Ri and Ga can pair up with any of the 6 combinations of Dha and Ni. Thus, there are 36 combinations of Ri – Ga with Dha – Ni that can go into the S – – M1 P – – S sequence, and the same 36 combinations can also go into the S – – M2 P – – S sequence, leading to a total of 72 different melodic scales, which are the melakartha ragas. The sequence is famously depicted as a chakra with concentric zones as shown below
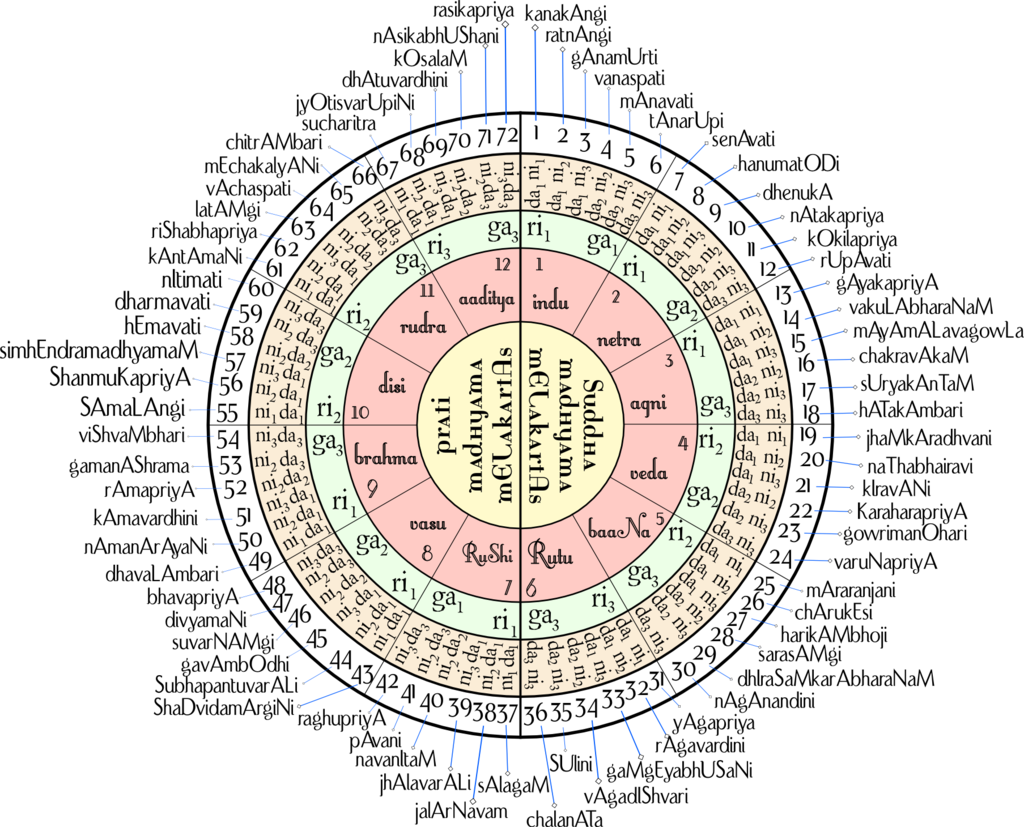 The melakartha chakra. The names listed outside the circle correspond to the 72 melakartha ragas. Photo taken from wikipedia article on Melarkartha. © Basavarajtalwar – Own work, CC BY-SA 3.0.
The melakartha chakra. The names listed outside the circle correspond to the 72 melakartha ragas. Photo taken from wikipedia article on Melarkartha. © Basavarajtalwar – Own work, CC BY-SA 3.0.
The above mela chakra is an easy way to depict the arrangement of the mela ragas. The circle is divided into two halves. The right half is the M1 or suddha madhyama side, and the left half is the M2 or the prati madhyama side. Thus all 36 ragas on the right half have S _ _ M1 P _ _ S as the notes, and the remaining 36 ragas of the mela sequence are featured on the left half with S _ _ M2 P _ _ S as the notes. As mentioned earlier, there are 6 different combinations of Ri and Ga, and 6 different combinations of Dha and Ni. These are depicted by the outer green and orange circular bands. The green band shows the combinations of Ri and Ga going clockwise in a repetitive sequence as R1G1, R1G2, R1G3, R2G2, R2G3, and R3G3. Recall that each of these can now form combinations with any of the 6 combinations of Dha and Ni. This is what the outer orange circular band represents, where each wedge has D1N1, D1N2, D1N3, D2N2, D2N3, D3N3 swara combinations going clockwise in a repetitive sequence.
Let’s now see how by merely knowing the name of raga, katapayadi equips us with an easy way to figure out the ascending and descending scales of that raga. The first two syllables in the name of each melakartha raga point to its number in the mela sequence. As an example, let’s take the popular raga चारुकेशि (charukeshi). The first two syllables च and र are encoding for the number 26 (when the numbers are read in reverse as per katapayadi decoding rule). Charukeshi is indeed the 26th raga in the mela sequence. Since 26 is less than half of 72, we can right away write down the four notes of the ascending and descending scales as S _ _ M1 P _ _ S. As for the remaining notes, each orange wedge has 6 notes in it. So going in multiples of 6, the 26th raga will fall in the 5th wedge which has R2 and G3 as the notes. The sequence of notes becomes S R2 G3 M1 P _ _ S. As for the two remaining notes, the 5th wedge has numbers starting from 25 and ending in 30. Thus, charukeshi, which is 26, will be second in the sequence of Dha and Ni combinations in that wedge. The full sequence of notes thus becomes S R2 G3 M1 P D1 N2 S. In this way, one can arrive at the ascending and descending scales of melakartha ragas by using katapayadi, without having to refer to any book. For a young student of music, doing this calculation mentally, in real-time, also serves as an exercise in basic arithmetic.
We conclude here by pointing out that there are a few exceptions to the above naming sequence, where the katapayadi decoded number does not point to the correct notes that define the raga [4]. How these anomalies have crept into the mela sequence remains an open question. For further historical notes on the nomenclature of the mela ragas, we encourage the readers to refer to chapter 6 of reference [5].
Embedding Dates Using Katapayadi
A classic use of katapayadi has been by authors to inscribe the date on which a text or a literary piece was completed. The date was embedded in a set of words within the same work. An excellent illustration of this is the hugely popular devotional hymn Narayaneeyam written by the celebrated mathematician and linguist Melpathur Narayana Bhattathiri in the sixteenth century CE. The final verse of the hymn goes as:

The concluding words of this verse are आयुरारोग्यसौख्यम् (āyur-ārogya-saukhyam). Taken literally, these words are a promise of longevity, health, and happiness that one would inherit by reciting the verses of the Narayaneeyam with devotion. Interestingly, the words ayur- ārogya-saukhyam is more than just a wish. Applying katapayadi to these words establishes the day on which Melpathur Narayana Bhattathiri completed the work Narayaneeyam. It gives the date in kali-ahargana or kali-dina-sankhya, which is the number of days since the start of the Kali Yuga as per the Malayalam calendar.
आ |
यु |
रा |
रो |
ग्य |
सौ |
ख्य |
म् |
0 |
1 |
2 |
2 |
1 |
7 |
1 |
– |
Kali Yuga started on February 18, 3102 BCE as per Surya Siddhantha (circa 800 CE). Narayaneeyam was written and completed 1712210 days after the start of Kali Yuga, which translates to December 8, 1586 CE in the Gregorian calendar that we follow.
A similar example is the mangalacaranam (invocatory verse) of the celebrated work tantrasangraha written in 1500 CE by Nilakanta Somayaji. The text starts with the following verse:

Here, the first set of words he vishno nihitham krisnam is katapayadi encoding of the number 1680548, which is the kali ahargana of when the text tantrasangraha was completed. Taking the starting of Kali Yuga to be February 18, 3102 BCE, we get the date of tantrasangraha as March 22, 1500 CE in the Gregorian calendar system.
What makes these examples truly fascinating is that the encryption of numbers was done without compromising the meaning of a verse or its poetic meter.
We close this essay by citing a few colloquial accounts of katapayadi encoding. These are examples rooted largely in the popular lore and are often not considered seriously by scholars as there is few documented evidence that serves to support or reject these as examples of katapayadi [2]. We mention them here because they are interesting.
The first example concerns the Mahabharata. The original name of the epic as given by its author Veda Vyasa, is Jaya. In katapayadi scheme, jaya codes for 18, a number that recurs in the epic·
- The Mahabharata is divided into 18 parvas or volumes.
- There are 18 chapters in the Bhagavad Gita which belongs to the Bhishma Parva (the sixth canto) of the Mahabharata
- The decisive battle of Kurukshetra lasted for 18 days
- In that war, 18 akshauhinis or army contingents participated
Along with highlighting the truth that in the grand scheme of things, the inevitable jaya or victory is always of dharma, the title also seems to point at a curious numerical pattern within the epic.
 The Mahabharata, narrated by Veda Vyasa, and scribed by Ganesha was originally called Jaya, a katapayadi encryption for the number 18, a number that recurs in the epic. Illustration by Prachi Prajapati
The Mahabharata, narrated by Veda Vyasa, and scribed by Ganesha was originally called Jaya, a katapayadi encryption for the number 18, a number that recurs in the epic. Illustration by Prachi Prajapati
Another equally interesting example is from the vishnu-sahasra-namam. This ever so popular hymn, featured in the anushana parva of the Mahabharata, extols a thousand names of Vishnu. Towards the concluding portions of the hymn, we find the following verse

where Parvathi asks Parameswara for ways to make the recitation of the thousand names of Vishnu quicker and easier for common scholars. To this Shiva replies:

that chanting Rama’s name thrice is equivalent to reciting a thousand names of Vishnu (rama-rama-rama ithi sahasranaama thathulyam). Interestingly the रा and म alphabets that make up the word राम have katapayadi values of 2 and 5 respectively. Mentioning राम thrice would thus amount to 2 x 5 x 2 x 5 x 2 x 5 = 1000 ! The Lord thus seems to have made a point here that is not just metaphysically true, but mathematically too.
Concluding Words
In this essay, we have touched upon only a few examples showcasing some of the ways in which this ancient art of encryption was put to use. Beyond everything else, katapayadi offers a glimpse into a past where knowledge was thought of and presented in a fundamentally unique way, in which seemingly diverse strands of human pursuit, be it language, philosophy, mathematics, music, fine arts, or science, were all blended into a single form, as though it is all one.
The people who wrote these brilliant works were polymaths; well-rounded intellectuals, whose competencies were unrestricted to any one topic. Through katapayadi, they created works with layers of meaning that one could peel into. Stashed within the eloquent poetry and prose of a text are often deeper philosophical reflections, and sometimes a mathematical truth or a scientific idea, for anyone who cared to probe.
Unfortunately, these fascinating accomplishments remain unfamiliar to many. Somewhere, the long thread that links the past to the present got broken. Finding a place for these knowledge traditions in our educational curriculum, by learning about them and sharing them with our children is perhaps a way to reconnect with the very roots of that wisdom, and to remind ourselves of the unique legacy we inherit.
Appendix I – Tabulation of Sine Values
We elaborate on how the following verse from Sankara Variya’s yuktidipika (16th century CE) is an encryption for the value of jya (i.e., Rsinθ) for angles from 0 to 90 degrees, uniformly increasing in steps of 3.75 degrees. In the penultimate line of the below verse, yuktidipika attributes the source of these jya values to Sangamagrama Madhava, who lived in Kerala during the 14th century CE.

The vakyas (sentences) in the above verse have a literal meaning. But they also have a numerical meaning coded in using katapayadi.
The words श्रेष्ठं नाम वरिष्ठानां (śreṣṭhaṁ nāma variṣṭhānāṁ) from the first line is katapayadi encryption for the number 224 arcminutes 50 arcseconds 22 sub-arcseconds (mathematically notated as 224ʹ 50ʹʹ 22ʹʹʹ).
श्र |
र |
ष्ठ |
म् |
ना |
म |
व |
रि |
ष्ठा |
म् |
ना |
म् |
– |
2 |
2 |
– |
0 |
5 |
4 |
2 |
2 |
– |
0 |
– |
Similarly, the second set of words हिमाद्रिर्वेदभावनः (himādrir-vēda-bhāvanaḥ) is katapayadi for 448ʹ 42ʹʹ 58ʹʹʹ, तपनो भानुसूक्तज्ञो (tapanō bhānu-sūktajñō) decodes as 670ʹ 40ʹʹ 16ʹʹʹ, and so on. How does this give the value of sine of angles?
A full circle subtends at its center an angle of 360 degrees, which is the same as 360 x 60 = 21,600 arcminutes. The radius of a circle with such a circumference would be
![]()
The sine value for the 24 wedges in succession according to the above verse is
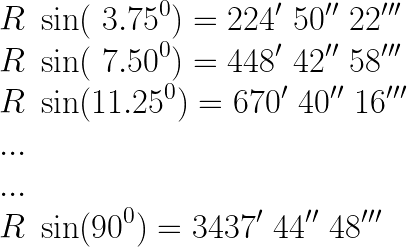
Dividing each of the above values of jya with the radius R, we get the values of the sinθ in succession, which are remarkably close to their true values.

In general, the sine trigonometric function values for any angle θ can be determined from the infinite series expression given by Madhava.
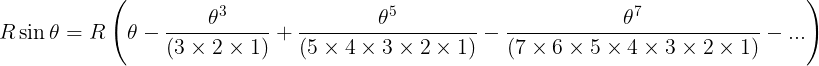
The above series involves an infinite number of terms. In practice, one does not need to expand the series endlessly. The series can be truncated after a couple of terms once the desired accuracy, in the value of sin θ, for the practical purpose is achieved. In karana-paddhathi written by Puthumana Somayaji (16th century CE), and in yuktidipika a further mathematical expression for the sine trigonometric function is mentioned, which also involves katapayadi. See sec 6.8 of reference [8].
References
[1] Dharampal, The Beautiful Tree: Indigenous Indian Education in the Eighteenth Century – Vol III, 1983, Other India Press, ISBN No.: 81-85569-50-9
[2] K V Sarma, Word and Alphabetic Numerical Systems in India, 2009, Essay published in Facets of Indian Astronomy (a collection of articles of Prof. K. V. Sarma), published by Rashtriya Sanskrit University, Ed. by Prof. Siniruddha Dash and Prof. Harekrishna Satapathy.
[3] Sreeramulu Rajeswara Sarma, The Katapayadi System of Numerical Notation, 2012, published in Revue d’histoire des mathématiques of the Société mathématique de France, volume 18, number 1, DOI : 10.24033/rhm.206
[4] V. Ramanathan & R. Venkateswara Pai, Decoding the Miscoded Raga Names in Carnatic Music, 2020, Proceedings of Indian National Science Academy, Vol. 86, No. 3, DOI: 10.16943/ptinsa/2019/49653
[5] P. Sambamoorthy, South Indian Musics (Book III), 1973, Indian Music Publishing House. E-copy available in https://archive.org/
[6] K. Ramasubramaniam, and M.S. Sriram, Tantrasangraha of Nilakanta Somayaji, (Sources and Studies in the History of Mathematics and Physical Sciences), Springer; 2011th edition, ISBN-13 : 978-0857290359. Also published by Hindustan Book Agency, ISBN-13 : 978-9380250090
[7] George Gheverghese Joseph, A Passage to Infinity: Medieval Indian Mathematics from Kerala and Its Impact, 2009, Sage India Publications, ISBN-13 : 978-8132101680
[8] V. Pai, K. Ramasubramanian, K., M. S. Sriram, M. D. Srinivas Karaṇapaddhati of Putumana Somayājī, 2018, Springer, ISBN -13: 978-9811068140
– ANAND NARAYANAN & NEENA SEKHARAN
Anand Narayanan teaches and does research in astrophysics at the Indian Institute of Space Science & Technology, Thiruvananthapuram. Neena Sekharan is based in Gurgaon where she works as a Risk Advisory Consultant.
The authors wish to thank Padma Vibhushan Dr. M. S. Valiathan for gifting a collection of Prof. K. V. Sarma’s articles on the mathematics and astronomy in ancient India which served as a valuable reference for this essay.
Disclaimer: The opinions expressed in this article belong to the author. Indic Today is neither responsible nor liable for the accuracy, completeness, suitability, or validity of any information in the article.