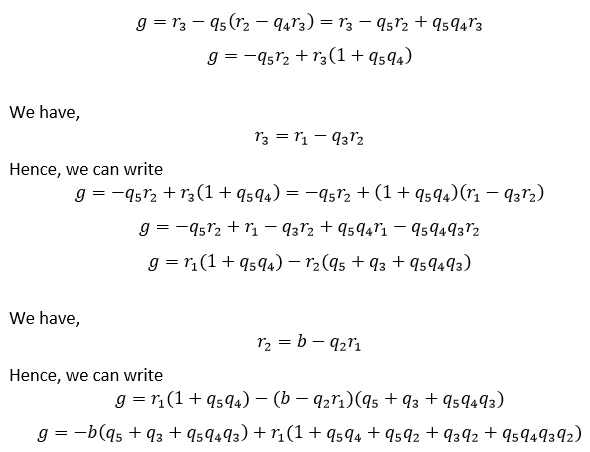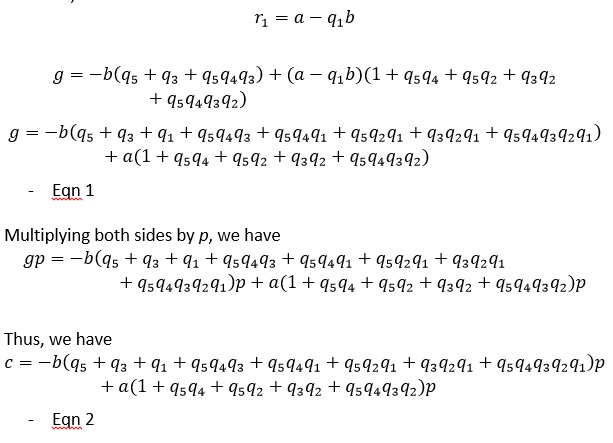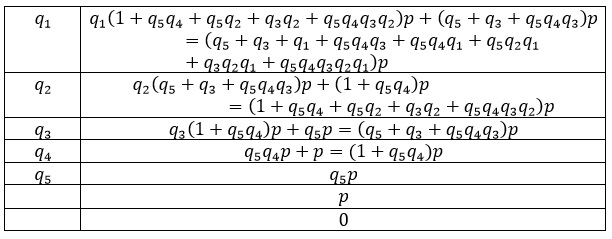शतं हतं येन युतं नवत्या विवर्जितं वा विहृतं त्रिषष्ट्या।
निरग्रकं स्याद् वद मे गुणं तं स्पष्टं पटियान् यदि कुट्टकेऽसि ॥२५१॥
(śataṃ hataṃ yena yutaṃ navatyā vivarjitaṃ vā vihṛtaṃ triṣaṣṭyā।
niragrakaṃ syād vada me guṇaṃ taṃ spaṣṭaṃ paṭiyān yadi kuṭṭake’si ॥251॥
One hundred is multiplied by an integer; 90 is added or subtracted from the product; the results are exactly divisible by 63. If you are proficient in kuttaka (pulverization), tell me the multiplier correctly (Find x)?
In my earlier article, I solved the above problem using an extension of Euclid’s GCD algorithm. In this article, I will solve the above problem using the ancient Indian kuttaka method. This method was first described by Aryabhatt. This method was also described by Mahavir in Ganitasarasangraha. This method was refined by Bhaskara II and described in both Bijaganita as well as Lilavati.
Kutta means to pulverize. In the kuttaka method we beat the problem into powder.
We have
Let a = 100 and b = 63.
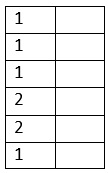
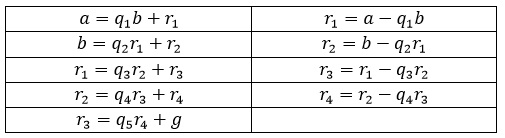
In the first stage of the kuttaka method we find the GCD of the two numbers 100 and 63, in the same way as the Euclid’s method.
1) 100 = 1 x 63 + 37
2) 63 = 1 x 37 + 26
3) 37 = 1 x 26 + 11
4) 26 = 2 x 11 + 4
5) 11 = 2 x 4 + 3
6) 4 = 1 x 3 + 1
7) 3 = 3 x 1 + 0
We have GCD(100, 63) = 1
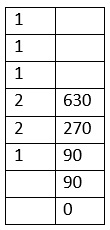
In the next stage of the kuttaka method, we list out the quotients up to the step where you get the GCD, in a column as shown below:
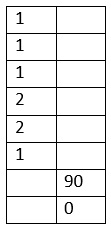
Then in the second column, in the row immediately below the one containing the last quotient, we write the constant in the given equation (90 in this case). And below that we write a zero. This is as shown below:
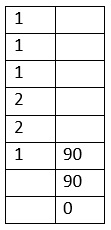
Now, we multiply the constant 90 with the last quotient 1 (i.e. the number immediately above it in the first column) and then add to the product the number just below it, 0 here. That is, (90 x 1) + 0 = 90. The result is written immediately above it. This is as shown below:
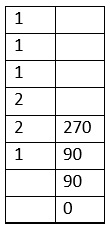
Now, we multiply the result 90 with the number immediately above it in the first column, that is 2, and then add to the product the number just below it, that is 90. This is, (90 x 2) + 90 = 270. The result, 270 here, is written immediately above it as shown below:
Now, we multiply the new result 270 with the number immediately above it in the first column, that is 2, and then add to the product the number just below it, that is 90. This is, (270 x 2) + 90 = 630. The result, 630 here, is written immediately above it as shown below:
This procedure is repeated till you fill up all the rows in the second column. This is as shown below:
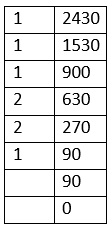
Using the top two numbers in the second column, we have
1530a – 2430b = -90
Here (1530, 2430) is one of the many solutions of the given equation.
(1530, 2430) is a solution with large numbers. Let us find a solution having the smallest positive values.
We have
If we divide xk by b, the remainder that we get will be the value of x1. Hence, let’s divide 1530 by 63. We get 18 as the remainder, which is the value of x1.
Also
If we divide yk by a, the remainder that we get will be the value of y1. Hence, let’s divide 2430 by 100. We get 30 as the remainder, which is the value of y1.
Thus, we have (18, 30) as one of the solutions for the given problem. Let’s verify this:
100(18) – 63(30) = -90
Some more solutions are: (81, 130), (144, 230), (207, 330), (-45, -70), (-108, -170)
For the equation, 100x – 63y = 90, (-18, -30) is one of the solutions. Let’s verify this:
100(-18) – 63(-30) = 90
Some more solutions are: (45, 70), (108, 170), (171, 270), (-81, -130), (-144, -230).
As compared to Euclid’s extended GCD algorithm the kuttaka method is easier, computable and quicker.
Let us now see why the kuttaka algorithm works:
We have
ax + by = c
Let GCD(a, b) = g and c = gp
Let us first enlist the steps to find the GCD(a, b).
Table 1
We can rewrite
as
We have,
Hence, we can write
We have,
Thus, we have
– Eqn 3
And
– Eqn 4
Now, let us apply the kuttaka method to the equation
ax + by = c = gp
I have enlisted the table for the kuttaka algorithm below:
Table 2
Comparing the top two entries in table 2 with eqn 4 and eqn 3 respectively, it becomes clear how the kuttaka algorithm works.
(Author’s Note: This article is a tribute to my Guru and mentor Late Prof. Bhalchandra A. Naik.)
Feature Image Credit: istockphoto.com
Disclaimer: The opinions expressed in this article belong to the author. Indic Today is neither responsible nor liable for the accuracy, completeness, suitability, or validity of any information in the article.