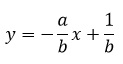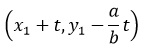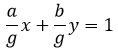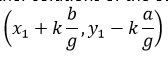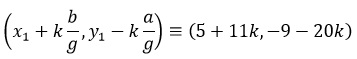(Euclid’s Extended Greatest Common Divisor Algorithm)
In continuation of the previous article, this piece carries the discussion forward…
शतं हतं येन युतं नवत्या विवर्जितं वा विहृतं त्रिषष्ट्या।
निरग्रकं स्याद् वद मे गुणं तं स्पष्टं पटियान् यदि कुट्टकेऽसि ॥२५१॥
(śataṃ hataṃ yena yutaṃ navatyā vivarjitaṃ vā vihṛtaṃ triṣaṣṭyā।
niragrakaṃ syād vada me guṇaṃ taṃ spaṣṭaṃ paṭiyān yadi kuṭṭake’si ॥251॥)
One hundred is multiplied by an integer; 90 is added or subtracted from the product; the results are exactly divisible by 63. If you are proficient in kuttaka (pulverization), tell me the multiplier correctly (Find x)?
The above problem is from Bhaskaracharya’s Lilavati. We will discuss the ancient Indian method of kuttaka in the next article. Here, we will solve the above problem using Euclid’s extended GCD algorithm.
We have,
Here, a, b and c are integer constants. And we want integral solutions for x and y.
Let GCD (a, b) = g. Here, both a and b are divisible by g, hence c will also be divisible by g.
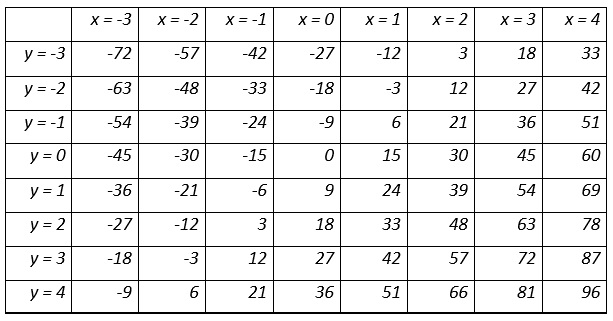
Hence, we can say that the values of the expression of type ax + by will always be a multiple of the GCD(a, b) = g. I illustrate this in Table 1 for the expression, 15x + 9y.
Table 1
Outputs of 15x + 9y for various values of x and y
We have
ax+by=c
Here, c is a multiple of g. Hence, we can write
ax+by=c=kg
If k = 1, then we have
ax+by=g
Here, g will be the smallest positive value for the equation.
For 15x + 9y, as can be seen from table 1, the smallest positive value is 3. Which is the GCD(15, 9).
The equation ax+by=c, will have multiple integral solutions. Equations having multiple solutions are called indeterminate equations. They are also called Diophantine equations after Diophantus (3rd CE), who used to study such equations. The given equation is linear; hence equations of this type are also called linear indeterminate equations or linear Diophantine equations (LDE).
As can be seen from table 1, 15x + 9y = 18 has more than one solution. For eg (0, 2) and (3, -3).
How do we solve the equation ax + by = GCD(a, b)?
If a and b are small, we might be able to guess the solutions. For, 15x + 9y = 3, we can easily guess that (-1, 2) and (2, -3) are the solutions.
If a and b are large it will be a very difficult task. We need to have an algorithm to solve the linear indeterminate equations.
An extension of Euclid’s GCD algorithm can solve the LDEs.
Let me illustrate this by solving
100x+63y=GCD100,63
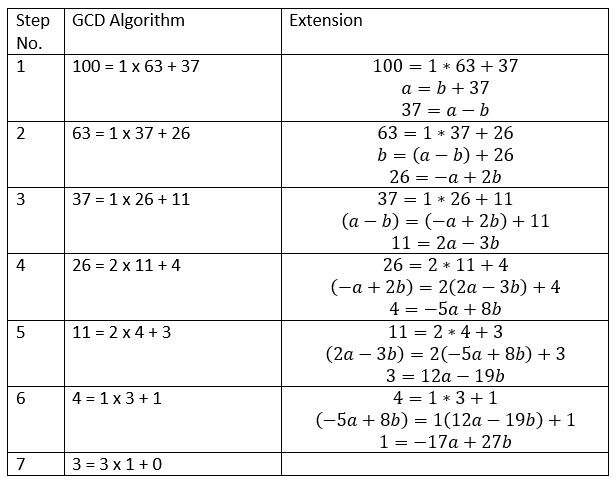
The first stage is to find the GCD (100, 63) by Euclid’s GCD algorithm.
- 100 = 1 x 63 + 37
- 63 = 1 x 37 + 26
- 37 = 1 x 26 + 11
- 26 = 2 x 11 + 4
- 11 = 2 x 4 + 3
- 4 = 1 x 3 + 1
- 3 = 3 x 1 + 0
Thus, we have the GCD(100, 63) = 1
Now to solve the LDE
100x+63y=1
We have, the first step of the GCD algorithm
100=1*63+37
a=b+37
Here, a = 100 and b = 63
37=a-b
We have, the second step of the GCD algorithm
63=1*37+26
b=a-b+26
26=-a+2b
We have, the third step of the GCD algorithm
37=1*26+11
a-b=-a+2b+11
11=2a-3b
We have, the fourth step of the GCD algorithm
26=2*11+4
-a+2b=22a-3b+4
4=-5a+8b
We have, the fifth step of the GCD algorithm
11=2*4+3
2a-3b=2-5a+8b+3
3=12a-19b
We have, the sixth step of the GCD algorithm
4=1*3+1
-5a+8b=112a-19b+1
1=-17a+27b
We stop the procedure when we get the GCD.
The coefficients of a and b will be the values of x and y respectively. Thus, we have one of the solutions for 100x + 63y = 1 as (-17, 27).
Let us verify the result:
100x + 63y = 100(-17) + 63(27) = -1700 + 1701 = 1
We can list all the above calculations in an elegant table as shown below in table 2.
Table 2
Here, in the extended GCD algorithm, we are expressing the remainder in every step in terms of the original two numbers, i.e. a and b.
Let (x1, y1) and (x2, y2) be two successive solutions of ax + by = 1. Here, GCD(a,b) is 1.
We have
ax+by=1
by=-ax+1
y2=y1-ka
Thus, we have
(x2,y2)≡(x1+kb,y1-ka)
By assigning various integer values to k, we can calculate various solutions to the given equation.
For 100x + 63y = 1, we have (-17, 27) as one solution. Now to calculate the successive solution we have (-17 + 63k, 27 – 100k).
Let, k = 1, we have
(x2,y2) = (-17+63,27-100) = (46,-73)
For, k = 2, we have
(x3,y3) = (-17+(2*63),27-(2*100)) = (109,-173)
From equation 1, we have
Geometrically we can visualise this as a line with slope as –(a/b). We can use (x1, y1) as a starting point to get the coordinates of new points. We have
For integer values of new coordinates t has to be a multiple of b. Let t = kb. Thus, we have
x1+kb,y1-ka
Looking at this from a different perspective:
We have
ax+by=1
Let (x1, y1) and (x2, y2) be two successive solutions of the equation. Then, we have
ax1+by1=1 – equation 4
ax2+by2=1 – equation 5
Equating equations 4 and 5, we have
ax1+by1=ax2+by2
ax2-ax1=by1-by2
a(x2–x1)=-b(y2–y1)
That is the difference in successive values of x will be equal to b and that of y will be equal to a. Thus, we can say that
x2–x1=-b
x2=x1-b
xk=x1-kb
and
y2–y1=a
y2=y1+a
yk=y1+ka
What if the GCD(a, b) > 1 ?
Let GCD(a, b) = g, then we have
ax+by=g
We can rewrite this has
Thus, we can calculate the other solutions of the equation by
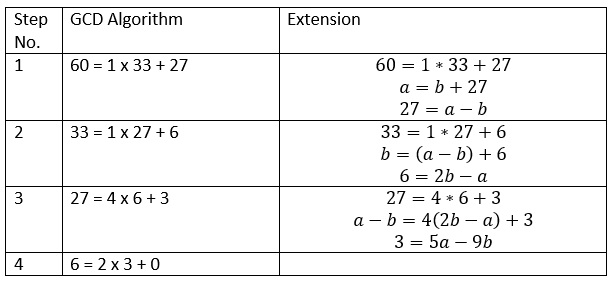
Let us solve one more linear indeterminate equation:
60x+33y=3
For the solution kindly refer to table 3.
We have
5a-9b=3
Thus, one of the solutions to the given LDE is (5, -9). Let us verify the solution:
60x + 33y = 60(5) + 33 (-9) = 300 -297 = 3
More solutions of the given LDE will be given by
Thus, we have (16, -29), (27, -49), (-6, 11), (-17, 31) and more.
Let us now look at how Euclid’s extended GCD algorithm works:
Let us begin with
As we move down line by line, we will continually be forming equations that look like
Last remainder = some multiple of a + some multiple of b
Here, in the extended GCD algorithm, we are expressing the remainder in every step in terms of the original two numbers, i.e. a and b.
This will continue till we reach the last non-zero remainder, which is the GCD (a, b). This will give us the desired solution for the LDE.
Let us now solve the problem from the Lilavati that is presented at the beginning of the article.
We have
100x – 63y = -90
We have found the solution for 100x + 63y = 1 which is (-17, 27). To find the solution for our current problem, we multiply 17 and 27 by 90. We get the numbers 1530 and 2430. Let’s verify this:
100(1530) – 63(2430) = -90
(1530, 2430) is a solution with large numbers. Let us find a solution having the smallest positive values.
We have
If we divide xk by b, the remainder that we get will be the value of x1. Hence, let’s divide 1530 by 63. We get 18 as the remainder, which is the value of x1.
Also
If we divide yk by a, the remainder that we get will be the value of y1. Hence, let’s divide 2430 by 100. We get 30 as the remainder, which is the value of y1.
Thus, we have (18, 30) as one of the solutions for the given problem. Let’s verify this:
100(18) – 63(30) = -90
Some more solutions are: (81, 130), (144, 230), (207, 330), (-45, -70), (-108, -170)
For the equation, 100x – 63y = 90, (-18, -30) is one of the solutions. Let’s verify this:
100(-18) – 63(-30) = 90
Some more solutions are: (45, 70), (108, 170), (171, 270), (-81, -130), (-144, -230)
In the next article we will solve LDEs using the ancient Indian method called kuttaka.
(Author’s Note: This article is a tribute to my Guru and mentor Late Prof. Bhalchandra A. Naik.)
Feature Image Credit: istockphoto.com
Disclaimer: The opinions expressed in this article belong to the author. Indic Today is neither responsible nor liable for the accuracy, completeness, suitability, or validity of any information in the article.