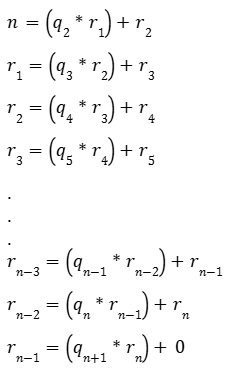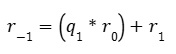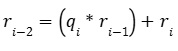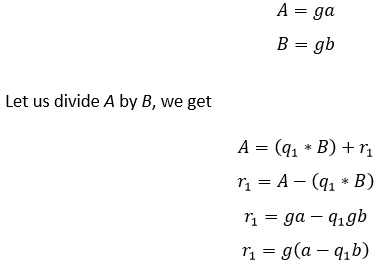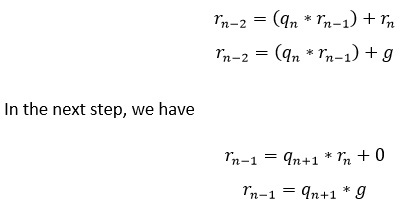(Mathematics has long been influenced by brilliant minds across cultures, and the ideas in this series of articles come from that history. Euclid laid the groundwork over two millennia ago with his algorithm for finding the greatest common divisor — a simple yet powerful principle that continues to influence mathematics today. In India, Āryabhaṭa presented the kuttaka (“pulverizer”) method to solve linear indeterminate equations, later described by Mahāvīra in his Gaṇitasārasaṅgraha and refined by Bhāskara II in works such as Bījagaṇita and Līlāvatī. Across three articles, we will explore Euclid’s algorithm, its mathematical logic, and its connection to the kuttaka tradition.)
Finding the Greatest Common Divisor (GCD) of two small numbers is pretty easy. But what if we have to find the GCD of two very large numbers like 3,87,205 and 12,903? Well, it is a very difficult and long procedure to find the GCD by the method one has learnt at school. Ancient Greek mathematician, Euclid (300 BCE), had given a quick and easy method to calculate the GCD of a pair of numbers.
Let us calculate the GCD of the above pair of numbers by Euclid’s method.
As a first step in the Euclid’s algorithm, divide the larger number by the smaller number as shown here:
387205 = (30 x 12903) + 115
We have 30 as the quotient and 115 as the remainder.
Now, as the second step of the algorithm, divide the smaller number by the remainder obtained above. We have
12903 = (112 x 115) + 23
As the next step, divide the previous remainder by the new remainder. We have
115 = (5 x 23) + 0
When we get zero as the remainder, the algorithm terminates. Here, the last non-zero remainder is the GCD.
Hence, we have GCD(387205, 12903) = 23.
Let us use this algorithm to find the GCD of another pair of integers 16,209 and 15,470.
16269 = (1 x 15470) + 799
15470 = (19 x 799) + 289
799 = (2 x 289) + 221
289 = (1 x 221) + 68
221 = (3 x 68) + 17
68 = (4 x 17) + 0
We have, GCD (16269, 15470) = 17.
Let us now generalise this by finding the GCD of a pair of integers m and n.
The first step of the algorithm will be
We can enumerate the steps of the algorithm as shown below:
Here, rn is the GCD of m and n.
If we let
![]() then, we have the first step of the algorithm has
then, we have the first step of the algorithm has
Now, the ith step in the algorithm can be represented as:
Does this algorithm give us the GCD?
Let us analyse this?
Is rn the common divisor of m and n?
Let us start from the bottom, that is the last step of the algorithm and work our way up.
The last step:
Here, we see that rn divides rn-1.
The penultimate step:
Here, rn divides both rn as well as rn-1. Hence, rn will also divide rn-2.
Now, the previous step:
We know that rn divides both rn-1 and rn-2, hence it will divide rn-3.
The step previous to this:
Here, rn divides both rn-2 and rn-3, hence it will divide rn-4.
In the same way, working our way up we reach the second step:
We know that rn divides both r1 and r2, hence it will also divide n.
Moving up to the first step, we have:
We know that rn divides r1 and n, hence it will divide m.
Thus, we establish that rn is a common divisor of m and n.
But how can we say that rn is the greatest common divisor?
Let d be any common divisor of m and n. From the first step of the algorithm, we have:
Since d divides both m and n, it will also divide r1.
Moving to the second step, we have
We now know that d divides r1 and n, hence it will also divide r2.
Moving to the next step, we have
We know that d divides r1 and r2, hence it will also divide r3.
Continuing down step by step when we reach the ith step, we have
From above, at every step we establish that d divides the previous two remainders, hence it will also divide the next remainder. Thus, we have that d divides both ri-2 and ri-1. Hence, we say that d also divides ri.
Eventually, when we reach the penultimate step:
We can say that d divides rn.
Hence, we can say that if d is any common divisor of m and n then d will divide rn. Therefore, we say that rn must be the GCD of m and n.
Will Euclid’s GCD algorithm always terminate?
In the first step, we have:
Here, r1 can have integer values between 0 to n-1.
In the next step, we have:
Here, r2 can have values between 0 and r1 – 1.
In the third step, we have:
Here, r3 can have values between 0 and r2 – 1.
We can see that with every successive step we have continually decreasing remainders. That is
r1 > r2 > r3 > …
Eventually we reach a step where the remainder equals 0. Hence, we can say that this algorithm always terminates.
How must Euclid have created his GCD algorithm?
Let g be the GCD of a pair of nonzero integers A and B, where A > B.
Let a and b be positive integers. Also let
Here a, b and q1 are integers. Hence, g is a factor of r1.
We have
Here g is a factor of A and B, hence we can say that g is also a factor of r1.
Now, let us divide the smaller number B by the first remainder r1. We have
From above, we know that g is a factor of (divides) both B and r1, hence we can say that g is also a factor of r2.
Now, let us divide r2 by r2. We have
We know that g divides both r1 and r2, hence it will also divide r3.
In the earlier article, I have explained that the successive remainders in this recursive procedure are decreasing. So, ultimately you will reach the step where the current remainder rn will become equal to the GCD, g. We have
This is the central idea behind how Euclid created the GCD Algorithm.
…Continued in Part 2
Feature Image Credit: istockphoto.com
Disclaimer: The opinions expressed in this article belong to the author. Indic Today is neither responsible nor liable for the accuracy, completeness, suitability, or validity of any information in the article.